3.1.1. Zusammenfassung

Zur Bereitstellung serienmässig produzierter Schäfte für eine grosse Anzahl unterschiedlicher Patienten müssen anatomische Abweichungen, die weitgehend unabhängige Gründe und ganz unterschiedliche Ausmasse haben, berücksichtigt werden. Wie zum Beispiel die Oberschenkellänge, die vor allem von der Grösse des Patienten abhängt, und der Markrauminnendurchmesser, der sich vor allem mit Alter und Aktivität des Patienten ändert.

Um dieses Ergebnis zu erreichen, müssen die Prothesenmasse (Breite, Länge, Dicke), die Halsmasse (Länge, Durchmesser) regelmässig von einer Grösse zur nächsten mit unabhängig für jede Grösse definierten prozentualen Werten ansteigen.

Das sind diese multiplikativen Faktoren (analog zu Zinssätzen), die ich seit 1981 „Wachstumsfaktoren“ oder „Growing Factors“ oder „GF“ nenne.

3.1.2. Die WachstumsFaktoren

Die WachstumsFaktoren bilden die Grundlage der mathematischen Methode, die ich speziell zur Berechnung von optimierten Implantatserien entwickelte. Diese Methode ermöglicht zudem eine gleichzeitige Berechnung sämtlicher Grössen der Serie.

Zur Bereitstellung optimaler in Serie und nicht individuell angefertigter Schäfte für eine grosse Anzahl unterschiedlicher Patienten müssen die anatomischen Abweichungen, die weitgehend unabhängige Gründe und ganz unterschiedliche Amplituden haben, berücksichtigt werden. Wie zum Beispiel die Oberschenkellänge, die in erster Linie von der Grösse des Patienten abhängt, und der Markraum innendurchmesser, der sich vor allem mit Alter und Aktivität des Patienten ändert.

Um ein zufriedenstellendes Ergebnis zu erreichen, müssen Länge, Breite und Dicke der Prothese sowie Halslänge und –durchmesser in regelmässigen Schritten von einer Grösse zur nächsten angehoben werden. Bei den Optimierten Grössen variiere ich alle Masse von einer Grösse zur nächsten mit Hilfe prozentual bestimmter und für jedes Mass unabhängiger Werte.

3.1.3. Vereinfachte Beispiele zur Bedeutung der Methode

Zur Vereinfachung der Erklärung möchte ich mich hier auf die Schaftlängen und Schaftbreiten sowie die Halslängen beschränken (andere Masse eignen sich weniger gut zur Demonstration).

Nehmen wir als Beispiel eine Serie mit 16 Grössen, die alle Patienten bedienen soll. Die Grösse der Patienten variiert zwischen 1,4 m und 2 m.

Vom grössten zum kleinsten Patienten ergibt sich folglich ein Variationsfaktor von 1,43 (43%). Diese Variation muss nun auf die 16 Grössen der Serie verteilt werden. Die den Markraumdurchmessern entsprechenden Schaftbreiten weisen für dieselbe Patientengruppe zwischen 6 mm und 30 mm variierende Werte auf. Dies entspricht einem Gesamtvariationsfaktor von 5 (400%), der ebenfalls regelmässig auf die 16 Grössen zu verteilen ist.

Würde der Längenfaktor von 1,43 auch zur Variierung der Breite verwendet, erhielte man Schäfte mit viel zu geringer Breitenvariierung (zum Beispiel zwischen 10 und 14 mm), die weder für Patienten mit einem Markraum von 6 mm noch für Patienten mit einem Markraum von 30 mm verwendet werden können.

Eine wirklich zufriedenstellende Lösung dieses Problems lässt sich durch eine lineare Intervallstaffelung zwischen der grössten und der kleinsten Grösse jeden Masses nicht erzielen.

Beispiel einer Schaftserie mit den Breiten 10, 12.5, 15, 17.5, 20. (Breiten der Zweymüller-Schäfte der ersten Generation). Zwischen 10 und 12.5 beträgt der Anstieg 25 %. Zwischen 17.5 und 20 beträgt der Anstieg nur 14.3 %.

Für einen Patienten, dessen Femur theoretisch einen Schaft der Grösse 12 benötigt hätte, existiert also nur die Grösse 10. Der Patient erhielte für seinen Femur eine um 20 % zu kleine Prothese. Diese mangelhafte Implantation beinhaltet eindeutig das Risiko eines Einsinkens der Prothese (dieser Fall ereignete sich mehr als 10 Mal in meiner Anwesenheit).

Ein Patient dagegen, für dessen Femur ein Schaft der Grösse 17 ideal wäre, erhält die verfügbare Grösse 15, die für seinen Oberschenkel also nur um 12 % zu klein ist. Dieser Patient ist damit „weitaus“ besser ausgestattet. Die Femurgrösse dieses Patienten hätte übrigens durch zusätzliche Raspelung ohne jedes Risiko auf 17.5 angehoben werden können. Bei dem kleinen Oberschenkelknochen des vorigen Beispiels wäre dies dagegen nicht möglich gewesen.

Bei einer kleinen Anzahl linear gestaffelter Grössen wird derjenige, der die Operation durchführt, von einem Patienten zum anderen zu völlig unterschiedlichem Handeln veranlasst. Kleine Patienten erhalten zudem häufiger unpassende Grössen.

Auf dem Markt existierten sogenannte „millimetrische“ Prothesen, die das Problem für den Patienten recht gut lösten, bei denen die Abstände zwischen den sehr grossen Grössen jedoch unnötig nahe beieinander lagen. Auch erforderten sie einen zu umfangreichen Bestand.

Ich forschte daher nach einem mathematischen Modell, das allen Patienten, dem kleinsten wie dem grössten, die absolut gleichen Chancen einräumt, möglichst annährend die ideale Grösse zu erhalten, mit einer bei allen Patienten konstanten Mangel- und Unsicherheitsrate. Derjenige, der die Operation durchführt, sollte zudem bei der Grössenauswahl für all seine Patienten das gleiche Verhalten beibehalten.

Ich bestimmte den Abstand zwischen zwei aufeinanderfolgenden Grössen dergestalt, dass derjenige, der die Operation durchführt, stets problemlos eine halbe Grösse zusätzlich oder notfalls auch etwas mehr raspeln kann. Das ist das Hauptprinzip des Konzepts der Optimierten Grössen.

3.1.4. Auswahl der WachstumsFaktoren

Zunächst bestimmte ich von allen Implantatsmassen diejenigen, die von einer zur nächsten Grösse variieren müssen und eine unabhängige Logik besitzen, und diejenigen, die eine in sich schlüssige Variationslogik besitzen.

Maximal 8 verschiedene WachstumsFaktoren schienen mir für die Berechungsmethode ausreichend.

1. wichtige Faktoren, die beispielsweise die Schaftbreite, die Länge der Knochenverankerungszone, die Halslänge und die AnteroPosteriore Dicke bestimmen

2. Faktoren, die zum Beispiel für die Veränderung des Halsdurchmessers am Konusbasis und der Ausmasse des Trochanterflügels verantwortlich sind

3. und eventuell Faktoren mit einem sekundären Nutzen, wie zum Beispiel der Durchmesser der Nahtlöcher, deren Veränderung zwar nur ästhetische Bedeutung hat, die der Serie jedoch einen positiven Eindruck der Kontinuität verleihen.

Einige zusätzliche Faktoren ergeben sich durch die lineare Kombination zwei der oben genannten Faktoren, die beispielsweise der Staffelung des Entwurfs der Distalspitzenbögen dienen.

Jedes Element der WachstumsFaktorenTabelle entsteht durch die sukzessiven Potenzen des jeweiligen für die 16 vorgesehenen Grössen des gewählten Wachstumsfaktors. Die mittlere Grösse dient als Ausgangspunkt für die Grössenstaffelung in beide Richtungen, nach oben und nach unten. Die Grössen überhalb der Mittelgrösse erhalten positive Potenzen des jeweiligen Wachstumsfaktors, die Grössen unterhalb erhalten negative Potenzen.

Falls erforderlich kann die Faktoren- und Grössenanzahl der Software erhöht werden.

Die vollständige Geometrie des Implantats ist in einem Informatikprogramm detailliert beschrieben, das für alle Grössen der Prothesenserie gilt. Das spezifische Beschreibungsprogramm einer Implantatserie beinhaltet ca. 4.000 Befehle. Für die Entwicklung dieser Implantate wurde kein Zeichenprogramm verwendet. Jeder Punkt und jede geometrische Einzelheit wurde mathematisch formuliert. Es wurde weder ein Näherungswert, noch eine Kurvenglättung oder ein automatisches Kurvenzeichnungssystem verwendet.

In meinem System werden alle Grössen gleichzeitig berechnet. Das Beschreibungsprogramm beinhaltet sämtliche Bezüge zwischen den aufeinanderfolgenden Grössen, während die Entwicklung der konkurrierenden Prothesen ausnahmslos mit Hilfe einer computergestützten Zeichensoftware erfolgt und eine Grösse nach der anderen entworfen wird. Zwischen den einzelnen Grössenabstufungen besteht keinerlei Bezug und die Masse werden manuell bestimmt und erfasst.

3.1.5. Das System verwendet gewisse Eigenschaften der Vektorräume

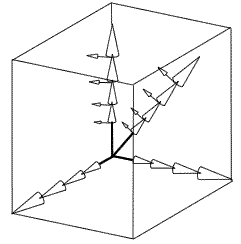
Statt der Berechnung einer dreidimensionalen Grössenserie in einem gewöhnlichen orthonormierten Raum, in dem die im rechten Winkel zueinander stehenden Vektoren auf der X-, Y- und Z-Achse die Länge der verwendeten Masseinheit besitzen (z.B. Millimeter), berechne ich die Serie der optimierten Grössen in einem Vektorraum mit 8 Dimensionen pro Grösse. Die 16 Potenzen jedes Wachstumsfaktors bestimmen 16 co-lineare Vektoren unterschiedlicher Länge. Die 8 Wachstumsfaktoren können 8 unterschiedlichen Richtungen im Raum zugewiesen werden, wobei einige im rechten Winkel zueinander stehen und andere in unabhängige Richtungen zeigen. So wird die Grössenserie des Beispiels in einem nicht orthonormierten Vektorraum mit 128 Dimensionen berechnet, der gleichzeitig die Koordinaten der 160.000 Punkte aller Grössen der Serie beeinhaltet.

Die erhaltenen Koordinaten werden in der sogenannten Koordinatenbasis gespeichert ( anders als der Parameterbasis). Da alle Implantatspunkte eine bekannte Position besitzen und nummeriert sind, können die Koordinaten zur Überprüfung oder Entnahme von Kontrollwerten für die Produktion jederzeit von den Tabellen abgelesen werden.

Nach Ende der Berechnungen wird jede Grösse selbstverständlich isoliert betrachtet und für die digitale Produktion in einen herkömmlichen orthonormierten 3 dimensionale Raum projiziert. Mit Hilfe meiner Software Transmission-Basis für die Übertragung zur Produktion können allein die für die Produktion nützlichen Koordinaten in der vom Hersteller erforderlichen günstigsten Anordnung extrahiert werden. Der Hersteller sorgt für die spezifische Anpassung an die digitale Verarbeitung. Die Beschreibung der Übertragung ist einzigartig und gilt für alle Grössen.

3.1.6. Grundlegende Wahl des Koordinatenursprungs

Dieser Methode liegt die Wahl des Vektorraums als gemeinsamer Ursprung und folglich der Koordinatenursprung zugrunde.

Hinsichtlich der Prothesenschäfte bestimmte ich das Wachstums- und Koordinatenzentrum am Schnittpunkt der Längenachse des Proximaldrittels und der theoretischen vom Zentrum des Femurkopfes und der durchschnittlichen Halsrichtung definierten Achse (dies gilt für einen symmetrischen Schaft, unsymmetrische Schäfte werden etwas anders behandelt).

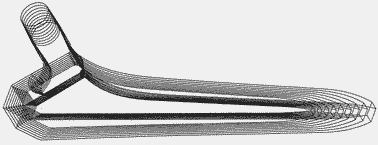
Bei einem nach der Methode der Wachstumsfaktoren konstruierten Implantat wird jedes Strukturdetail von einem oder mehreren der 8 zur Verfügung stehenden Wachstumsfaktoren bestimmt. Beispielsweise die 45°-Abschrägungen der SL-Plus-Schäfte entlang der gesamten Verankerungszone an den 4 Ecken des rechteckigen Schnitts werden ebenfalls mit Hilfe von Wachstumsfaktoren bestimmt und erfüllen die Prinzipien der Konischen Kupplung und des Aufsteigenden Einschachtelungs bis auf den Mikrometer genau.

Die Breite dieser Schrägkanten nimmt von der Distalspitze bis zum Proximalabschnitt regelmässig zu und variiert bei jeder Grösse. In keinem Fall handelt es sich um mit Hilfe einer graphischen Software automatisch eingeführte Abschrägungen oder Kantenabrundungen mit konstanten Massen. Das Verhältnis zwischen diesen Abschrägungen und der entsprechenden Form der Raspelzähne ist von grosser Bedeutung und soll gesondert dargelegt werden.

Im Gegensatz zu manchen prmitiven Behauptungen wurde die Serie der SL-Schäfte folglich nicht durch Homothetie oder photographische Vergrösserung, das heisst mit einem einzigen in allen Raumrichtungen konstanten Faktor, hergestellt.

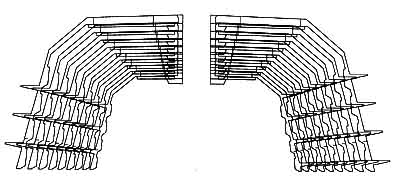
3.1.7. Vergleich zwischen Zweymüller SL Schaft und dem Müller Geradschaft

Als Beispiel hier der ohne Wachstumsfaktoren entworfene gerade Schaft von Müller: die Länge des Metallhalses ist für alle Größen konstant, der Kopf ist fest und der Operateur verfügt über keinerlei Ausgleichsmöglichkeit für die verbleibenden Gelenkspannungsabstände nach Zementverhärtung.

Bei den Varianten und zahlreichen Imitationen der selbstblockierenden Prothesen von Müller mit austauschbaren Köpfen war die konstante Länge des Metallhalses zu lang für die kleinen Größen und zu kurz für die großen Größen.

Die kurzen, mittleren und langen Hälse der Modularköpfe werden zum Ausgleich des fehlenden Halsunterschiedes verwendet und stehen folglich nicht mehr für die letzten Gelenkspannungskorrekturen zur Verfügung.

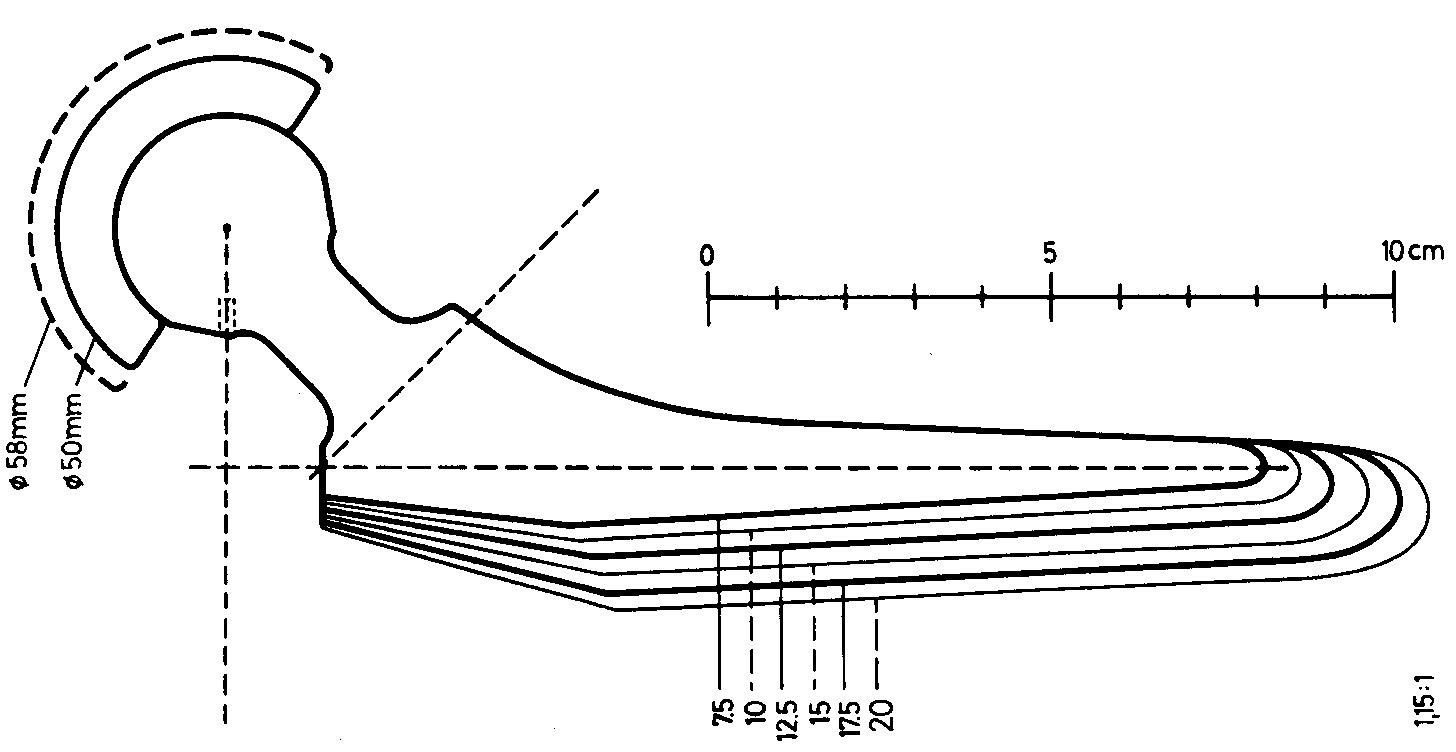
In meinem bei den Zweymüller-Prothesen angewandten Konzept variieren die Metallhälse regelmäßig und müssen die Köpfe mit kurzen, mittleren und langen Hälsen dem Ausgleich der verbleibenden Gelenkspannungsabstände vorbehalten werden.

----

Die Methode der Optimierten grössen

Inhaltsverzeichnis