4.8.1. Zusammenfassung

Von Anfang an besitzt die Verankerungszone der Zweymüller-Schäfte der drei Generationen rechteckige Schnitte.

Wären die Proportionen des Schnittrechtecks bei der gesamten Serie der AlloClassic-Schäfte und SL-Plus-Schäfte identisch beibehalten worden, wäre der obere Teil des Schafts der Größe 12 ungeheuer dick und unnötig steif und die Distalspitze des Schaftes der Größe 1 dagegen lächerlich dünn und hätte die Schäfte sehr kleiner Größe zu zerbrechlich werden lassen.

Zur Beseitigung dieses Problems entwickelte ich eine mathematische Methode, dank derer die Dicken aller Größen auf allen Ebenen der Basispyramiden kontinuierlich verändert werden konnten. Die Methode verringert die Dicke des oberen Teils von Größe 12 und verdickt die Spitze der kleinsten Größe, um so eine Annäherung an einen quadratischen Schnitt zu erreichen, der den besten mechanischen Widerstand für einen gegebenen Durchmesser bietet.

Mit Hilfe dieser Dickekorrektur können die Methoden der Aufsteigenden Einschachtelung und der Optimierten Größen angewandt werden und erweist sich der Ausdruck “alle Schäfte der Serie scheinen aus einem einzigen Metallblock geschaffen zu sein” nach wie vor als wahr.

4.8.2. Anwendung von Dickenkorrekturen auf Schäfte mit rechteckigem Querschnitt.

Eine Entwicklung der Serie der SL-Schäfte von 1984 unter Beibehalt gleichbleibender Proportionen für die Verankerungszonen aller Grössen wäre einfach gewesen.

Manche vertraten irrtümlich die Meinung, dass die SL-Schäfte homothetisch anstiegen . Behielte man gleichbleibende Proportionen bei, mit dem gleichen Formfaktor für den Querschnitt aller Grössen und entlang aller Schäfte, und wählte den Formfaktor der dafür angemessenen Durchschnittsgrösse, erwiesen sich die kleinen Schäfte, wie beispielsweise die Grössen 1 und 2, auf Grund des äusserst flachen rechtwinkligen Querschnitts als extrem zerbrechlich.

Das gleiche gilt für die grossen Grössen 11 und 12. Würde man den Formfaktor deren Querschnittes mit dem Formfaktor der Mitte der Durchschnittsgrösse identisch halten, bekämen diese Schäfte ein ungeheuer grosses Gesamtvolumen und hätten zudem die bei Titan ohnehin geringe Elastizität verloren.

Mit derartigen Problemen waren die Urheber der Zweymüller-Prothese der ersten Generation nicht konfrontiert. Alle Schäfte besassen eine konstante Dicke von ca. 9mm, vom Schaft „10“ bis zum Schaft „17,5“, als seien sie alle aus der gleichen 9mm dicken Titanblechplatte geschnitten worden. Natürlich verringerte sich diese Dicke entlang des Schaftes ein wenig, allerdings mit zufallsbedingten Winkeln, die weder definiert noch berechnet wurden.

Diese Überlegungen waren sieben Jahre später bestätigt durch die Vergleichende Studie zum mechanischen Widerstand der Spotorno- und Zweymüller-SL-Schäfte von Manfred Semlitsch, Sulzer, 1991. Die in dieser Studie aufgezeigten Unterschiede sind teils auf die „verzerrte“ Messmethode zurückzuführen. Diese ist das Ergebnis einer Neigung des Schaftes um 10 Grad, von vorne nach hinten, bei der Befestigung in der Experimentanordnung.

4.8.3. Dickenkorrekturen sind mit dem Prinzip der Aufsteigenden Einschachtelung kompatibel.

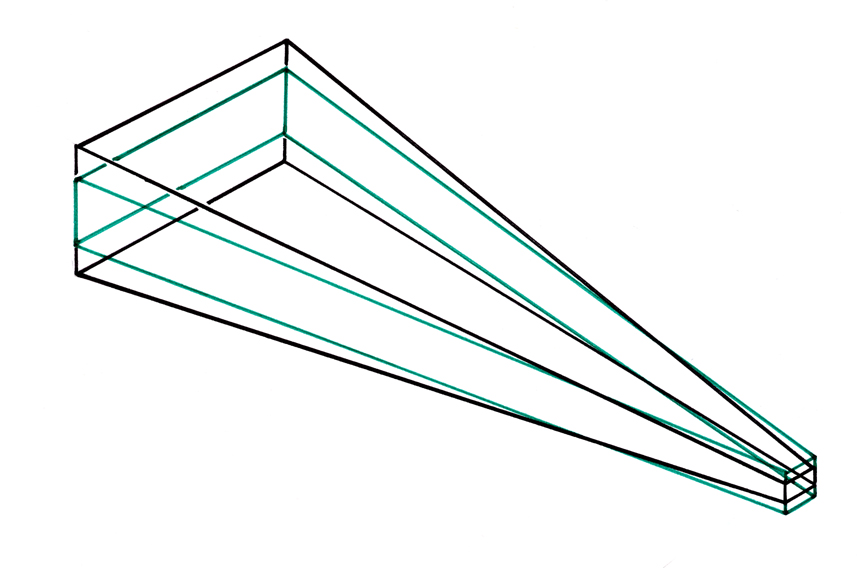
Um das Prinzip des Aufsteigenden Einschachtelung zu erfüllen, werden alle Grössen der SL-Schäfte auf unterschiedlichen Ebenen und mit unterschiedlichen Längen durch Berechnung in eine einzige und gleiche geometrische Hülle extrahiert. Diese stellt schematisch eine virtuelle Titanstange dar, aus der alle Schäfte geschnitten würden.

4.8.4. Mathematischer Aspekt der Dickenkorrekturen

Die SL-Schäfte und später die SL-Plus-Schäfte besitzen vor den Berechnungen zur Dickekorrektur einen konstanten Formfaktor.

Dieser Formfaktor ist das Ergebnis einer Gestaltungsentscheidung und kommt auf der mittleren Ebene der Durchschnittsgrösse der Schaftserie zur Anwendung. Er ist ein Element der Parameterdatenbank.

Ich verwende hier folgende Definition: Verhältnis zwischen 0 und 1 zwischen der langen und kurzen Seite eines Rechtecks und allgemeiner des um die Linien einer beliebigen Form beschriebenen Rechtecks, wobei die lange Seite in Richtung des grössten Durchmesser zeigt.

De plus, pour les tiges SL-plus et SLR-plus, l'angle n'est pas constant et varie un peu tout le long de la tige du fait d’une fraction du “ Polynôme du Calcar ” proportionnelle au Facteur de Forme à chaque niveau, appliqué également aux faces antérieure et postérieure. Cette variation d'angle est visible à l'oeil nu pour les tiges SLR-Plus et Holz-Zacher par exemple.

Einige Marketingredakteure lieferten frei erfundene Winkelwerte, ohne mich um die geringste Information zu ersuchen. Ich selbst kenne den exakten Wert dieses Winkels nicht, da er aus einer automatischen Computerberechnung hervorgeht, die zahlreiche Parameter des Schafts einbezieht.

4.8.5. Die Dickenkorrekturen bearbeiten den Pyramidalen Basisform

Die Berechnungen zur Korrektur der Dicke werden auf die Grundformen mit konstantem Formfaktor angewandt und ermöglichen eine mässige und progressive Entfernung von diesen Grundformen, um den Abschnitt an der Distalspitze der kleinsten Seriengrösse so gut wie viereckig und den Proximalabschnitt der grössten Grösse relativ flach zu halten.

Folglich besitzen die ganz kleinen Schaftgrössen den bestmöglichen mechanischen Widerstand für kleine Titanmasse (Artikel von Dr. Semlitsch) und sind die sehr grossen Grössen, bei denen wenige Probleme in Bezug auf mechanischen Widerstand zu befürchten sind, nicht so gigantisch.

4.8.6. Exemple de formulation paramétrée des Corrections d'Epaisseur

Die Übersetzung der kodierten Formulierung in gängige Sprache ermöglicht die Identifizierung der bei der Berechnung der Dickekorrekturen verwendeten Parameter:

Iteration über 16 Grössen

Dicke1 = FormFaktor x .5 x ( WachstumsFaktor1,Grösse1 )

Dicke2 = FormFaktor x .5 x ( WachstumsFaktor1,Gmittel ) + Formfaktor x ( WachstumsFaktor2,GrösseReferenz ) x Tangente halber Winkel Vorderseite

Korrektor1 = ProximalKorrektor x ( ( Dicke2 - FormFaktor x halbe ProximalBreite, GrösseLaufend ) / ( Dicke2 - Dicke1 ) )

Korrektor2 = ProximalKorrektor x ( ( FormFaktor x halbe ProximalBreite,GrösseLaufend - Dicke1 ) /( Dicke2 - Dicke1 ) )

Halbe korrigierte ProximalDicke = ( halbe ProximalBreite,GrösseLaufend ) x FormFaktor + ( Korrektor1 + Korrektor2 ) / 2

Korrektor3 = ProximalKorrektor x ( ( Dicke2 - FormFaktor ) x ( halbe DistalBreite, GrösseLaufend ) / ( Dicke2 - Dicke1 ) )

Korrektor4 = DistalKorrektor x ( (FormFaktor x halbe DistalBreite, Tlaufend - Dicke1 ) / ( Dicke2 - Dicke1 ) )

halbe DistalDicke = DistalBreite x FormFaktor + halber Korrektor3 + halber Korrektor4

4.8.7. Das Ergebnis bildet die erste Term des Calcar-Polynoms

Nach Anwendung der Berechnungen zur Dickekorrektur auf alle Schäfte der Serie erhält man die Pyramidale Basisform der Verankerungszonen.

Diese Umrisse bilden das erste Element des Calcar-Polynoms des SL-Plus-Schafts. Die Verankerungszone der AlloClassic-Schäfte entstand allein durch die vorhergehenden Formen.

Figur: Schematische Darstellung der einzigartigen mittels Dickekorrekturen behandelten Titanstange.

----

Die Einschlagreserve bei den Raspeln

Inhaltsverzeichnis