4.8. The Thickness Corrections
4.8.1. Summary
Right from the start, the anchoring zone of the Zweymüller stems of the three generations has rectangular sections.
If the proportions of the section rectangle were preserved identical for all the series of AlloClassic stems and SL Plus, the top of the stem of size 12 would be monstrusly thick and unnecessarily rigid and on the other hand the distal point of the stem of size 1 would have been ridiculously thin and would have made the stems of very small size too fragile.
To eliminate this problem, I developed a mathematical method allowing to modify uninterrupted the thicknesses of all the sizes on all the levels of the Pyramidal Base. The method thins the thickness top of size 12, and thickens the point of the smallest size to bring it closer to a square section, which gives the best mechanical resistance for a given diameter.
This thickness correction makes it possible to respect the methods of Ascending Interlocking and Optimized Sizes and the expression” all the stems of the series seem to be extracted from the same single metal block” remains true.
4.8.2. Application of the Thickness Corrections to the stems of rectangular section
It would have been easy to carry out the series of stems SL of 1984 by preserving constant proportions of the zones of anchoring for all the sizes.
Some could believe that stems SL grew in a homothetic way, which is an error. If one preserved constant proportions, with the same Form Factor for the cross section for all the sizes, and all along each stem, by taking the Form Factor of the intermediate size which proved to be suitable, the stems of small size, such as for example sizes 1 and 2, would be extremely fragile because of the very flat rectangular section.
It is the same for big sizes 11 and 12. If the Form Factor of their section had been maintained identical to that of the medium of the intermediate size, these stems would become monstrous in total volume and moreover the little of elasticity which Titanium allows would have lost.
These problems had not arisen to the Authors of Zweymüller first generation. All the stems had a constant thickness of approximately 9mm, stem “10” with the stem “17.5”, as if they all had been cut out in the same Titanium sheet plate of 9mm thickness. Of course this thickness decreased a little along the stem, moreover with random angles, neither definite nor calculated.
These reflections were confirmed seven years later by the comparative study of the mechanical resistances of the stems Spotorno and Zweymüller SL by Manfred Semlitsch, Sulzer, 1991. The differences highlighted in this study were partly due to the method of the measurement “in torsion”, which is obtained by the tilted fixing of 10 degrees into antéro-posterior of the stem in the experimental construction.
4.8.3. The Thickness Corrections are compatible with the Principle of Ascending Interlocking
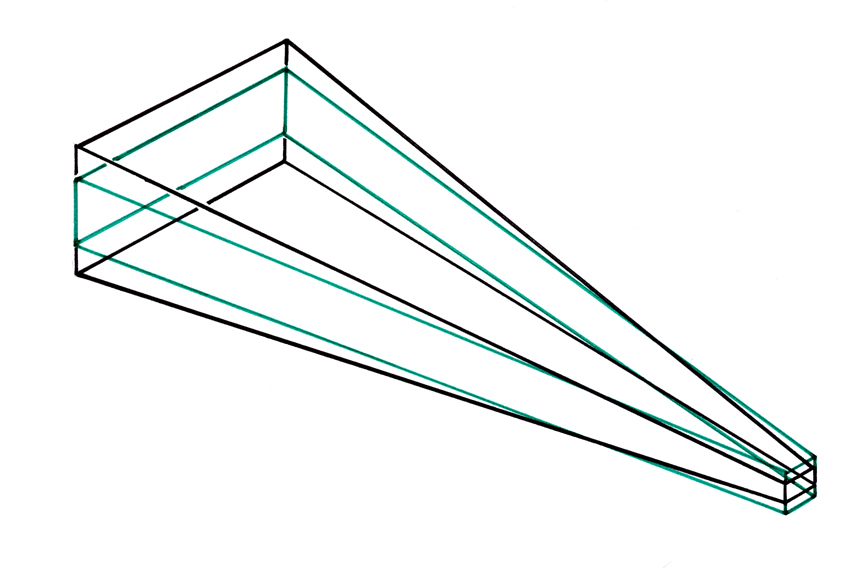
To satisfy the principle of Ascending Interlocking, all the sizes of stems SL, are extracted by calculation, on different levels and with different lengths, in same and single geometrical envelope schematizing a virtual Titanium bar in which all the stems would be cut out.
4.8.4. Mathematical aspect of the Thickness Corrections
Stems SL, then thereafter SL Plus, have, before the application of calculations for the Thickness Correction, a constant Form Factor.
This Form Factor results from a decision of design and applies at the average level of the intermediate size of the series of stems. It is an element of the Parameter Base.
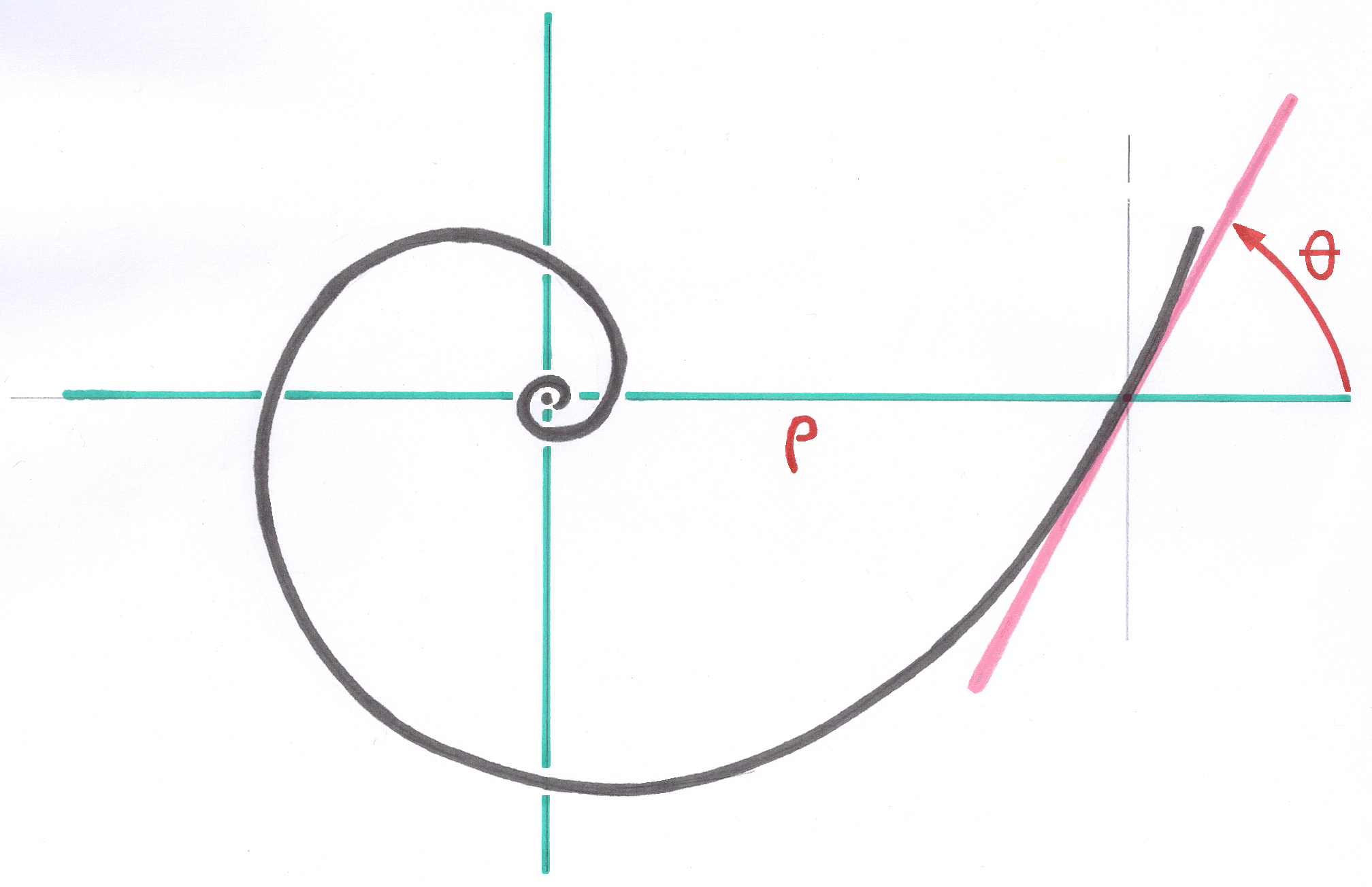
I use the following definition here: relationship ranging between 0 and 1 between the small side and the large side of a rectangle, and more generally of the exinscrit rectangle around a flat contour of an unspecified form, the large side being in the direction of the larger diameter.
I do not know myself the value of this angle because it is the result of an automatic data-processing calculation utilizing many parameters of the stem.
Moreover, for the stems SL-Plus and SLR-Plus, the angle is not constant and varies a little all along the stem because of a fraction of the “Polynomial of Calcar” proportional to the Factor of Form on each level, also applied to the former and posterior faces. This variation of angle is visible with the naked eye on the stems SLR-Plus and Holz-Zacher for example.
Certain marketing writers indicated whimsical angular values, without me to ask for least information. I myself don't know the exact value of this angle because it comes from an automatic computer calculation that takes into account numerous parameters of the stem.
4.8.5. The Thickness Corrections treat the Pyramidal Base Form
Calculations of Thickness Corrections applied to Pyramidal Base Form having a constant Form Factor, to make it possible to deviate, moderately and gradually, of these base form so that the section with the distal point of the more small size of the series is practically square, and that the proximal section of the biggest size is relatively flattened.
This way, the very small sizes of stems will have the best possible mechanical resistance for low-size of Titanium (article of Dr. Semlitsch) and the very big sizes will be less colossal the more so as few problems of mechanical resistance are to be feared.
4.8.6. Example of parameterized formulation of the Thickness Corrections
The translation of the coded formulation into common language allows the identification of the parameters used in the calculation of the thickness corrections:
Loop on 16 sizes
Thickness1 = FormFactor x .5 x ( GrowthFaktor1,Size1 )
Thickness2 = FormFactor x .5 x ( GrowthFaktor1,SizeMedium ) + Formfactor x ( GrowthFactor2,SizeMedium ) x Tangent half FrontAngle
Corrector1 = ProximalCorrector x ( ( Thickness2 - FormFactor x ( half ProximalWidth, CurrentSize ) /Thickness2 - Thickness1 ) )
Corrector2 = ProximalCorrector x ( ( FormFactor x half ProximalWidth,CurrentSize) - Thickness1 /( Thickness2 - Thickness1 ) )
Half corrected ProximalThickness = ( half ProximalWidth,CurrentSize ) x FormFaktor + ( Corrector1 + Corrector2 ) / 2
Corrector3 = ProximalCorrector x ( ( Thickness2 - FormFactor x half DistalWide, CurrentSize ) / ( Thickness2 - Thickness1 ) )
Corrector4 = DistalCorrector x ( (FormFactor x half DistalWidth, CurrentSize - Thickness1 ) / ( Thickness2 - Thickness1 ) )
half DistalThickness = DistalWidth x FormFactor + halfCorrector3 + half Corrector4
4.8.7. The result provides the first term of the Calcar Polynom
After application of Thickness Corrections calculations to all the stems of the series, one obtains the Pyramidal Base Form of the anchoring zones.
These are the contours which will constitute the first term of the Calcar Polynom of stem SL Plus. The anchoring zone of the AlloClassic stems was only consisted the forms previously obtained.
Diagrammatic representation of the single Titanium bar treated by the Thickness Corrections.
----