2.3. Le Principe de Jonction Conique dans l'Os
2.3.1. Résumé
L’Ancrage Géométrique nécessite une Jonction Conique.
Les tiges fémorales à Ancrage Géométrique sont immobilisées dans l’os de la même façon que les assemblages mécaniques à jonction conique impactée, dite cône morse, comme le sont par exemple toutes les têtes prothétiques modulaires.
La zone d'ancrage de la tige et le lit osseux préparé doivent satisfaire les définitions mathématiques des cônes.
Le lit osseux doit être préparé par râpage ou alésage pour présenter face à l'implant une proportion suffisante de surface rectifiée.
La surface de l'implant doit présenter une rugosité ou microstructure de surface assurant le blocage de la Jonction Conique.
Une Réserve d'Impaction doit être prévue lors de la préparation de l'os pour permettre la mise en précontrainte de l'os lors de l'impaction définitive.
2.3.2. Comment sont définis les cônes
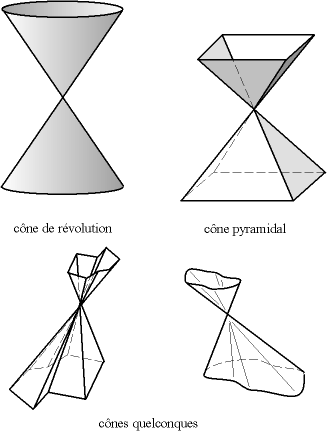
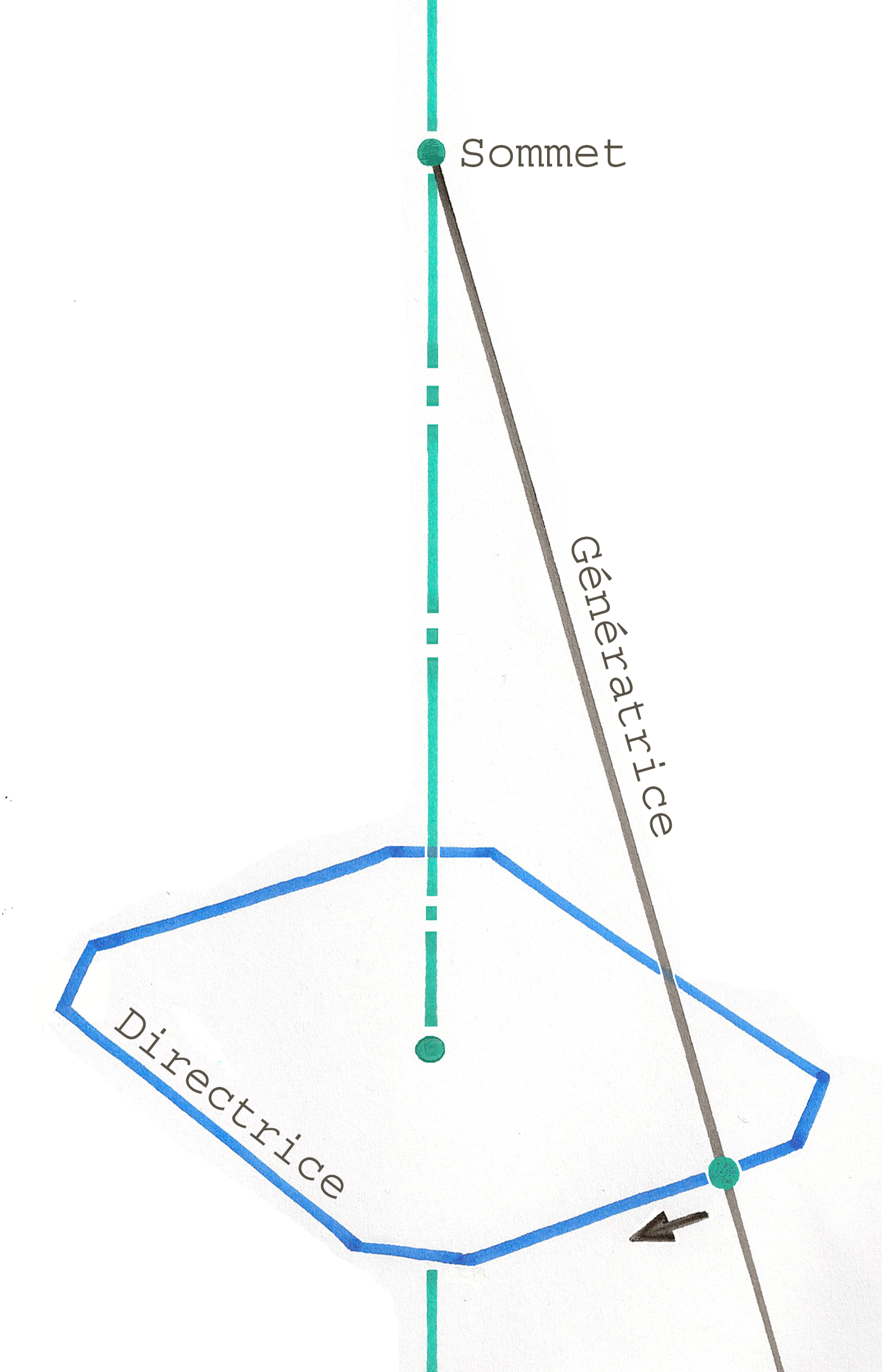
Un cône est la surface réglée décrite par une droite appelée génératrice, passant par un point fixe appelé sommet et un point variable parcourant une courbe plane fermée, appelée courbe directrice. On parle aussi dans ce cas de surface conique.
Cône de révolution Parmi les surfaces coniques, la plus habituelle est le cône de révolution dans lequel la courbe directrice est un cercle perpendiculaire et centré sur l'axe passant par le sommet. Ce cône est appelé de révolution car il peut être généré simplement par la rotation d'une droite passant par le sommet et inclinée d'un angle fixe par rapport à l'axe.
C'est à partir de ce cône de révolution que les mathématiciens (dont Apollonius de Perga) ont classifié un ensemble de courbes comme les coniques (intersections du cône par un plan) : cercles, ellipses, paraboles, hyperboles. (wikipedia)
2.3.3. Généralisation de la notion de jonction conique
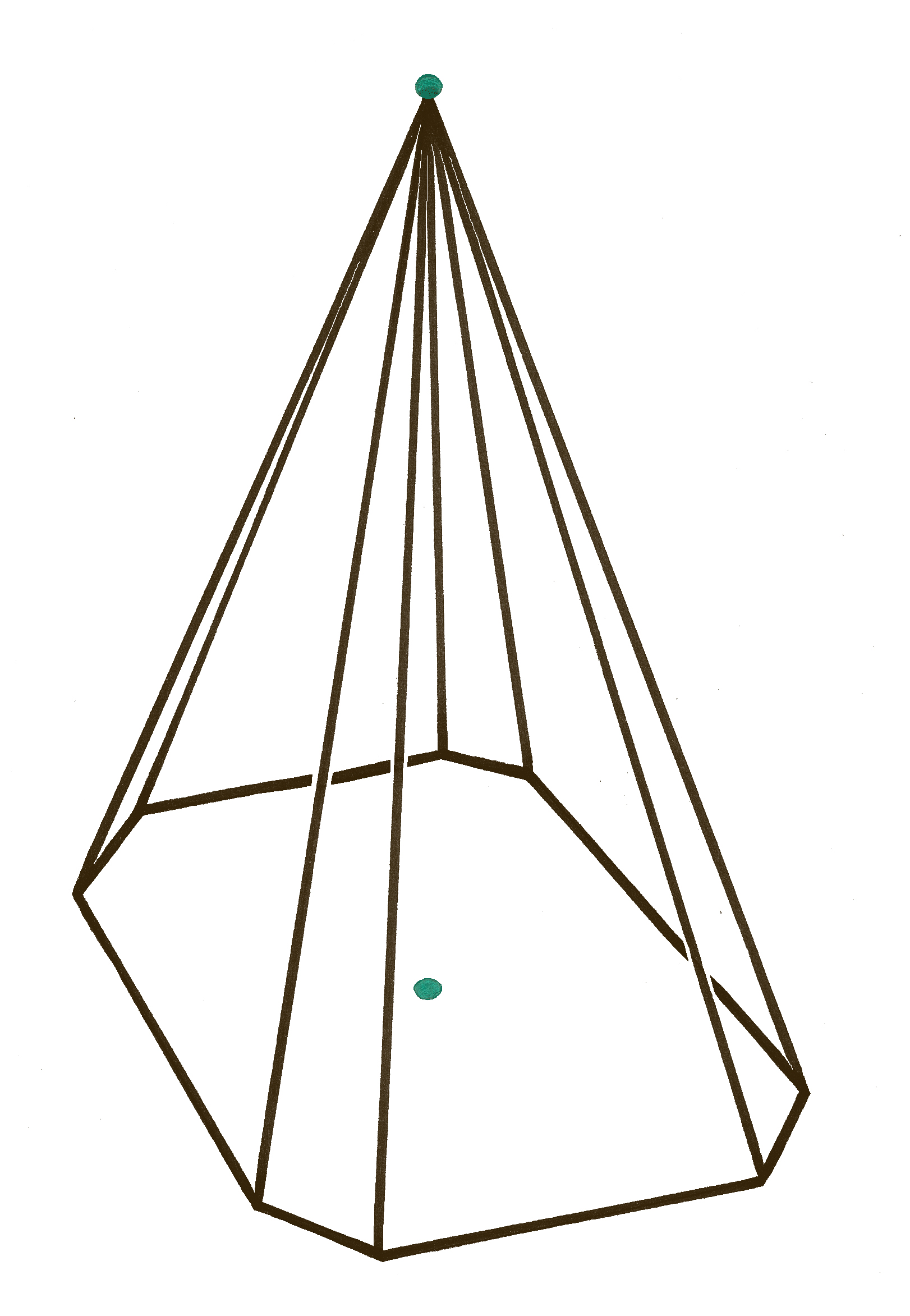
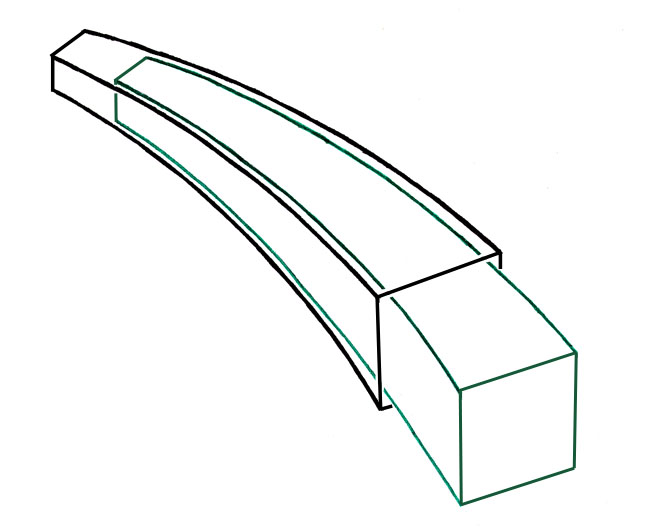
Les jonctions coniques impactées sont traditionnellement obtenues par des surfaces en présence en forme de tronc de cône de révolution. Les jonctions coniques peuvent également être obtenues avec des surfaces pyramidales, donc des surfaces coniques ayant des sections rectangulaires ou carrées et même avec des directrices de formes plus complexes.
C'est en cherchant à transformer la prothèse de Zweymüller de première génération qui était plutôt en forme de " coin ", en lui appliquant les règles mathématiques de la forme pyramidale que j'ai commencé le perfectionnement de cette tige et abouti à la prothèse AlloClassic en 1984, et SL Plus en 1992.
2.3.4. L'assemblage os-prothèse par jonction conique
Les surfaces coniques appliquées d'une part à l'os, d'autre part à l'implant, doivent toujours satisfaire la définition mathématique du cône. Dans certains cas des adaptations spécifiques peuvent s'avérer intéressantes. Les angles de blocage, les états de surface et les propriétés de friction des matériaux associés souvent très différents, doivent être convenablement définis.
Comme pour toute jonction conique, les surfaces en présence ne doivent jamais être lisses, et doivent nécessairement comporter des rugosités aléatoires, ou des microstructures fines géométriquement définies. Ces surfaces s’incrustent l’une dans l’autre, la microstructure du matériau le plus dur agressant la surface du matériau le plus tendre. Cette incrustation supprime le risque de glissement axial qui risquerait de relâcher la tension élastique (précontrainte) initialement établie par l'impaction.
Dans le cas de l'ancrage géométrique d'une tige dans l'os, c'est le titane sablé par des cristaux de corindon qui agresse microscopiquement le matériau le plus tendre, l’os cortical.
La stabilité par blocage des tiges à jonction conique est obtenue par deux actions logiques successives:
1. D'une part l’insertion de l’implant dans son lit osseux ( les surfaces théoriques mâle et femelle étant seulement mises en contact ) à la place strictement nominale du point de vue géométrique et dimensionnelle.
Cela signifie que pour les deux surfaces coniques, tous les points destinés à venir en contact se rencontrent sans qu'il y ait encore, dans cette phase, de forces ou de pressions (précontrainte) qui aient pris naissance.
C'est seulement dans la phase logique suivante que tous ces points seront simultanément soumis à des forces localement perpendiculaires aux surfaces. Ces forces seront, en principe, égales en tous points mais pourront différer de façon modérée et contrôlée par l'application calculée de petites différences dans la forme des surfaces (ces effets sont obtenus par les Fonctions de Fixation et de Séparation dans le calcul des tiges SL-plus et SLR-Plus).
Je pense que cette constance des forces reste toujours une première approximation, car même dans le cône morse traditionnel ces forces ne sont pas rigoureusement constantes du fait de la différence des diamètres à deux niveaux différents et donc de la différence des taux de compression.
2. D’autre part une impaction supplémentaire. Après que la géométrie exacte des deux pièces ait été atteinte, cette impaction supplémentaire procure une mise en tension réciproque des deux pièces en présence, la pièce mâle étant comprimée et la pièce femelle étant dilatée. Cette mise en tension apporte la stabilité définitive de la jonction.
De petits écarts en linéarité ou en courbure générale entre la tige et le fourreau osseux, de l’ordre du millimètre, sont également absorbés par des déformations minimes des deux composants, permises par les élasticités du titane de la tige et de l’os cortical de la diaphyse. Ces déformations élastiques de faible amplitude participent au blocage conique et contribuent à la stabilité primaire de la prothèse. Elles participent à la mise en précontrainte et, dans un deuxième temps, stimuleront l’Ostéointégration de la tige.
2.3.5. La Réserve d’Impaction est indispensable
Pour que cette impaction supplémentaire soit possible, sans risque de blocage, et sans risque de fissure, la préparation de la cavité osseuse doit présenter la même forme que la tige sur toute la longueur de la zone d'ancrage, mais se prolonger un peu plus profondément que la pointe distale de la tige et ne pas s’arrêter strictement à la profondeur de la pointe théorique de la tige. Cela constitue la Réserve d'Impaction pour une tige diaphysaire.
Il serait inadmissible que l'impaction supplémentaire soit rendue impossible par un rétrécissement prématuré du lit osseux qui empêcherait la tige d'être impactée des quelques millimètres indispensables pour établir la mise en précontrainte.
En l’absence de la Réserve d’Impaction, on ne peut parler que d’un assemblage instable de deux pièces de forme conique. C'était le cas de l'assemblage de la coque monoconique AlloPro et de son insert en polyéthylène qui laissait toujours un jeu entre le pièces.
Le blocage distal prématuré, faute de réserve d'impaction, se produisait souvent avec les tiges Zweymüller de première génération ( 1979-1985 ) et avait plusieurs fois provoqué des instabilités extrêmement douloureuses ayant nécessité des réopérations.
La râpe d’une taille donnée doit préparer l’os 5 à 10 mm plus profondément que la tige correspondante pour qu’en aucun cas ne persistent un rétrécissement et une région non préparée au voisinage de la pointe de la tige.
Quand la Réserve d'Impaction est préparée, la tige ne sera pas bloquée à sa pointe distale, lors de sa mise en place, au fond de la préparation, par le brusque rétrécissement du canal médullaire.
Le lit osseux, après impaction définitive de la tige, est mis en Précontrainte avec des forces qui s’exercent de la façon la mieux répartie possible le long des lignes de contact primaire entre la tige et le canal médullaire, les pressions s'exerçant perpendiculairement aux surfaces en présence, en chaque point de contact, selon le concept des Contraintes réparties.
----
