3.5. L'Espace Courbe en Spirale Logarithmique.
3.5.1. Résumé
Dans le but de développer des implants courbes s'incorporant mieux que des tiges à axe rectiligne dans des diaphyses elles-mêmes courbes, mais qui satisfont tous les principes de l'Ancrage Géométrique, j'ai effectué une étude mathématique aboutissant à une conclusion unique : seules des tiges calculées dans un espace courbe en spirale logarithmique peuvent satisfaire cette exigence.
Ne disposant d'aucune source antérieure, j'ai développé une méthode mathématique nouvelle pour décrire ces implants.
Deux familles de tiges fémorales courbes ont été conçues dans l'Espace Courbe en Spirale Logarithmique: Les tiges Modular Plus de réopération profonde, et la famille des tiges du projet Anatomica.Nova couvrant toutes les gammes: de première intention, de réopération et de réopération profonde.
Par ailleurs, j'ai poussé le développement plus loin pour la conception de l' "Alésoir Spiral Inverse " qui sert à l'implantation des tiges courbes de réopération profonde à ancrage géométrique Modular Plus. La description de cet instrument très original sera développée plus loin.
3.5.2. Ancrage Géométrique et implants courbes
Des implants possédant toutes les propriétés de l'Ancrage Géométrique semblaient ne pouvoir être réalisés qu'avec des axes principaux rectilignes. En me posant la question : est-il possible de satisfaire les conditions de l'Ancrage Géométrique avec des tiges courbes, j'en suis arrivé aux observations suivantes :
3.5.3. L'axe curviligne en arc de cercle est inadapté à l'Ancrage Géométrique.
Un implant, dont l'axe curviligne et les contours seraient des portions de cercles, ne satisfait jamais mathématiquement les principes de l'Ancrage Géométrique. Toute tentative de créer un implant avec un axe curviligne circulaire entraînerait des approximations trop grossières. Le Principe de la Jonction Conique dans l'os ne serait pas satisfait.
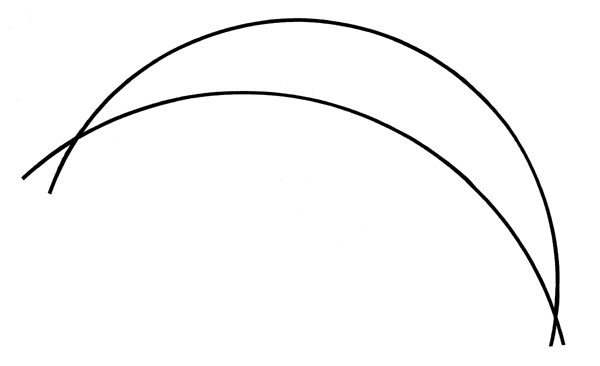
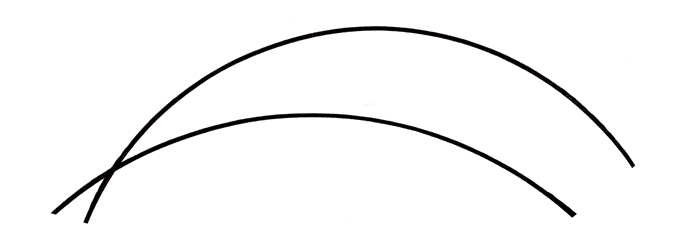
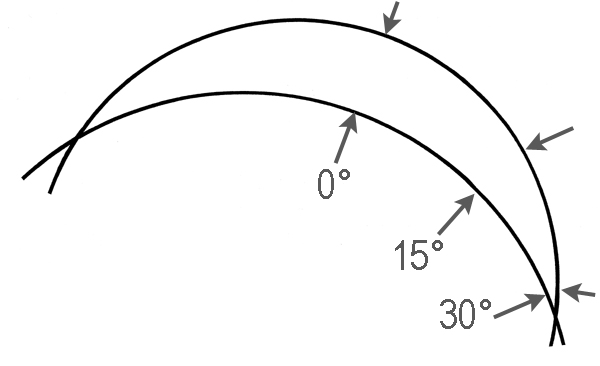
Si l'on tente de schématiser une jonction conique d'axe curviligne circulaire en représentant le contour de la tige par deux arcs de cercle qui présentent deux points d'intersection, on voit de façon évidente que l'angle des tangentes en deux points face à face sur les deux cercles ne reste constant en aucune région de ces cercles.
Aux deux points d'intersection, cet angle est maximal alors que, si l'on s'éloigne d'un point d'intersection, les cercles deviennent progressivement parallèles et finissent même par se rejoindre au deuxième point d'intersection. On imagine aisément que l'adjonction de la troisième dimension à cette géométrie schématique ne permettra pas davantage de réaliser une quelconque jonction conique courbe.
3.5.4. La Spirale Logarithmique.
A ma connaissance, ce problème a une solution mathématique unique. Cette solution est apportée par la Spirale Logarithmique qui a la propriété de présenter, tout le long de la courbe, un angle constant (Theta) entre la tangente en un point de la spirale et le Rayon-Vecteur (Ro) reliant ce point au Pôle Asymptotique de cette spirale.
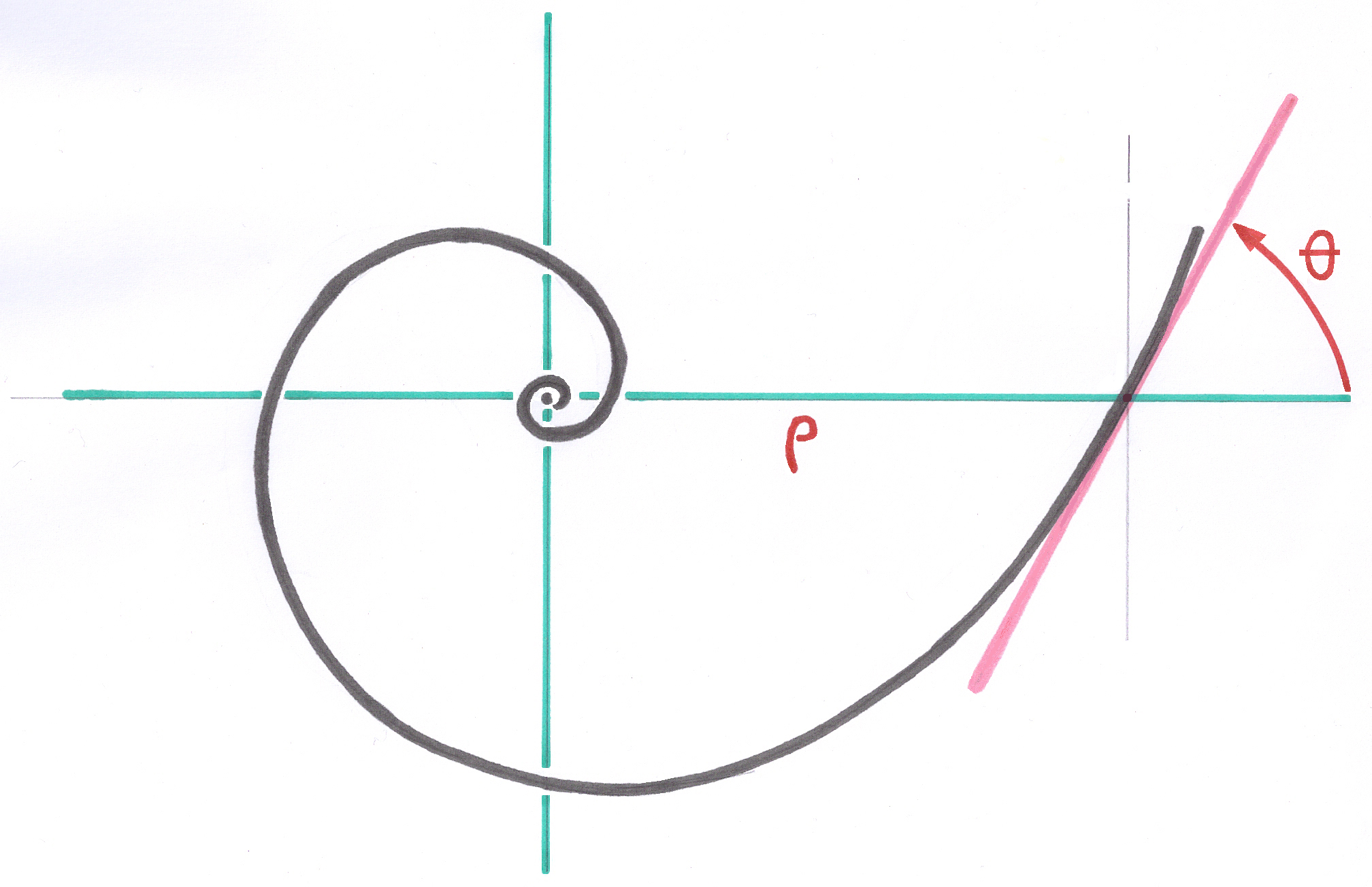
Les multiples approximations graphiques plus ou moins grossières des spirales, utilisant des arcs de cercle successifs et croissants, et que l'on trouve dans tous les articles de la Littérature et sur Internet sous le mot Spirale et même Spirale Logarithmique, ne conviennent que pour la décoration, mais pas pour créer scientifiquement des implants et des jonctions coniques courbes.
Je dois rendre hommage à Monsieur Dupin, normalien, mon Professeur de Mathématiques Spéciales, qui m'a transmis cette compréhension mais aussi l'aptitude à la généralisation.
3.5.5. La Spirale Logarithmique à 3 dimensions.
Me souvenant de la propriété remarquable des spirales logarithmiques de conservation des angles mais n'ayant rien trouvé dans les livres au sujet des extensions de la spirale logarithmique à la troisième dimension, j'ai dû mettre au point les méthodes, les formulations et enfin la transposition en langage informatique, pour pouvoir appliquer rigoureusement, sans arrondis et sans lissages, les propriétés de la spirale logarithmique aux tiges prothétiques courbes.
J'ai appelé " Espace Courbe en Spirale Logarithmique " la géométrie globale dans laquelle tous les points de l'implant sont calculés. Afin de pouvoir transmettre ces points à la fabrication sur machines numériques, je reviens à la géométrie classique en projetant chacun de ces points dans l'espace euclidien orthonormé.
C'est ensuite que j'ai remarqué que la plupart des mollusques, escargots, moules et autres, sont décrits dans un espace Spiral Logarithmique, de même les galaxies, malgré quelques perturbations.
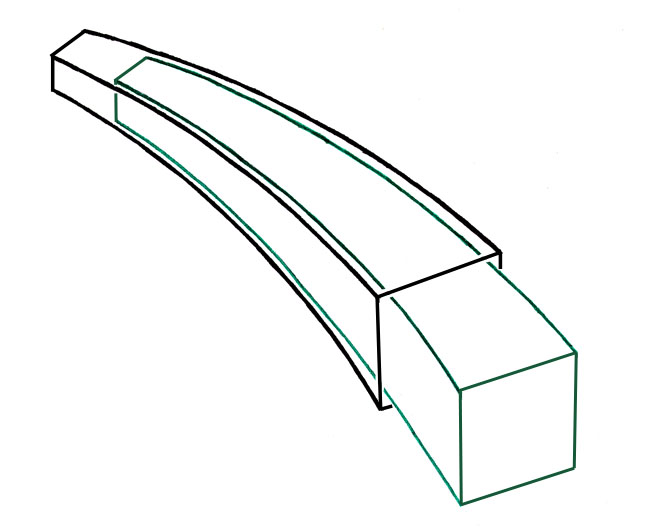
Seul un implant décrit dans un Espace Courbe en Spirale Logarithmique possède la propriété de jonction conique courbe. Tous les implants courbes qui ne sont pas calculés avec cette géométrie sont incompatibles avec l'Ancrage Géométrique.
J'ai développé deux groupes d'application de la spirale logarithmique :
3.5.6. Le groupe des tiges.
Le premier, dont l'axe curviligne est dans un plan.
Cet axe curviligne sert de référence à chaque niveau de découpage le long de l'axe, a un espace orthonormé local dans lequel sont définis tous les points appartenant à ce niveau. Les arêtes des tiges destinées à venir en contact avec les parois osseuses préparées par râpage ou alésage spiral sont également des spirales logarithmiques, en 3 dimensions, s'éloignant régulièrement de l'axe curviligne et faisant des angles constants avec cet l'axe. C'est ce premier groupe qui est à la base des différentes familles de tiges courbes que j'ai eu l'occasion de mettre au point.

En annexe 6.3.5. texte intégral de mon brevet FR 96 01539. du 08.02.1996
3.5.7. Le groupe des alésoirs.
le deuxième groupe possède un axe curviligne tridimensionnel à spires multiples, décrit dans un espace dans lequel les coordonnées en Z des points résultant du découpage sont elles mêmes distribuées selon une fonction logarithmique. C'est ce groupe d'espaces courbes qui m'a permis de développer l' " alésoir spiral " destiné à remplacer les râpes pour l'implantation des tiges de réopération profonde Modular Plus.
En annexe 6.3.7. texte intégral de mon brevet EP 0 788 772. du 08.02.1996
3.5.8. Discrétisation de l'axe curviligne.
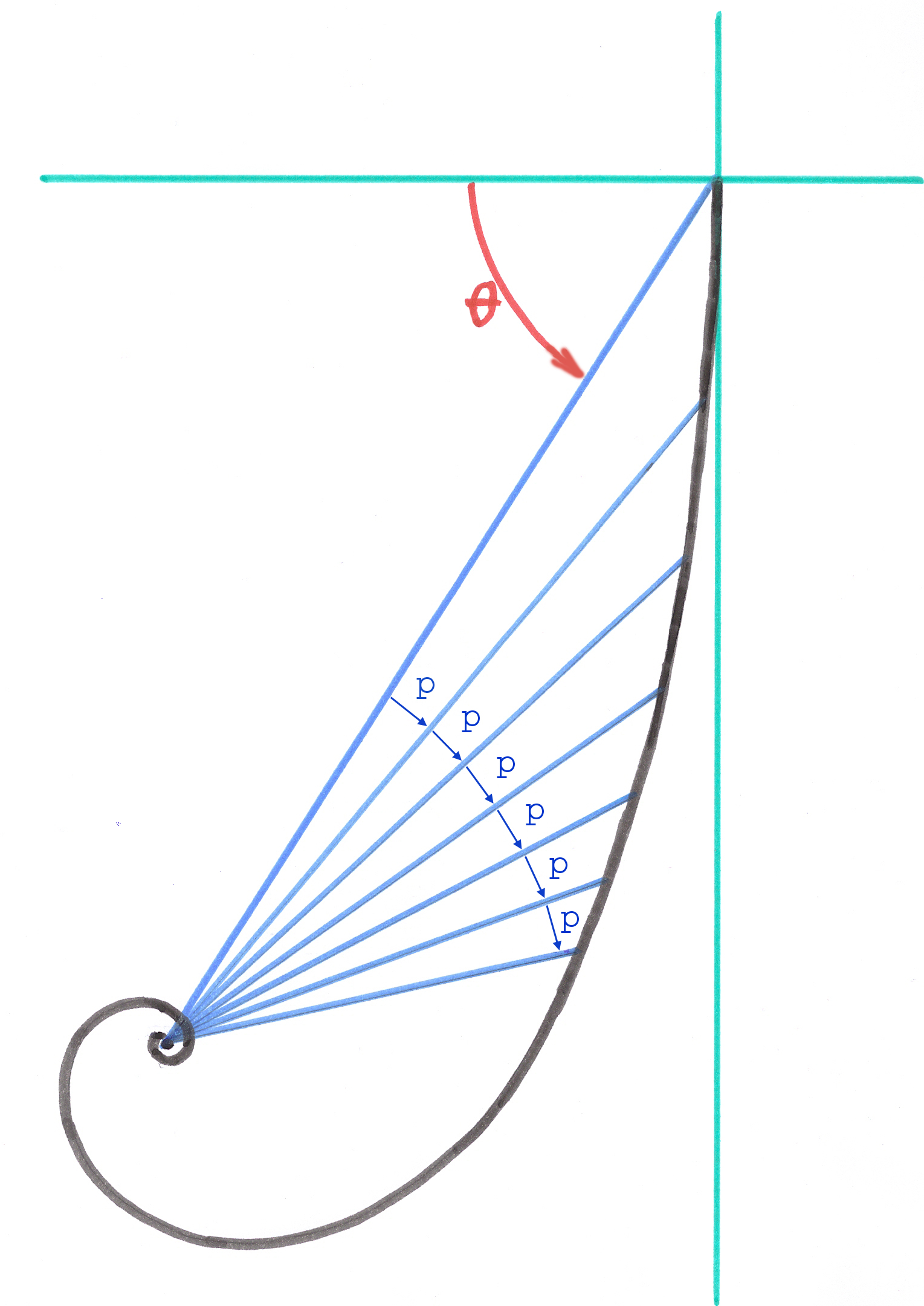
Le découpage de ces courbes le long des axes curvilignes n'a pas lieu de façon linéaire mais par des pas angulaires constants effectués par le rayon-vecteur provenant du pôle de la spirale et rencontrant l'axe curviligne.
La courbure totale des implants courbes calculés par cette méthode doit se limiter à environ 0,2 radian.
3.5.9. Description d'un objet dans un espace courbe en spirale logarithmique.
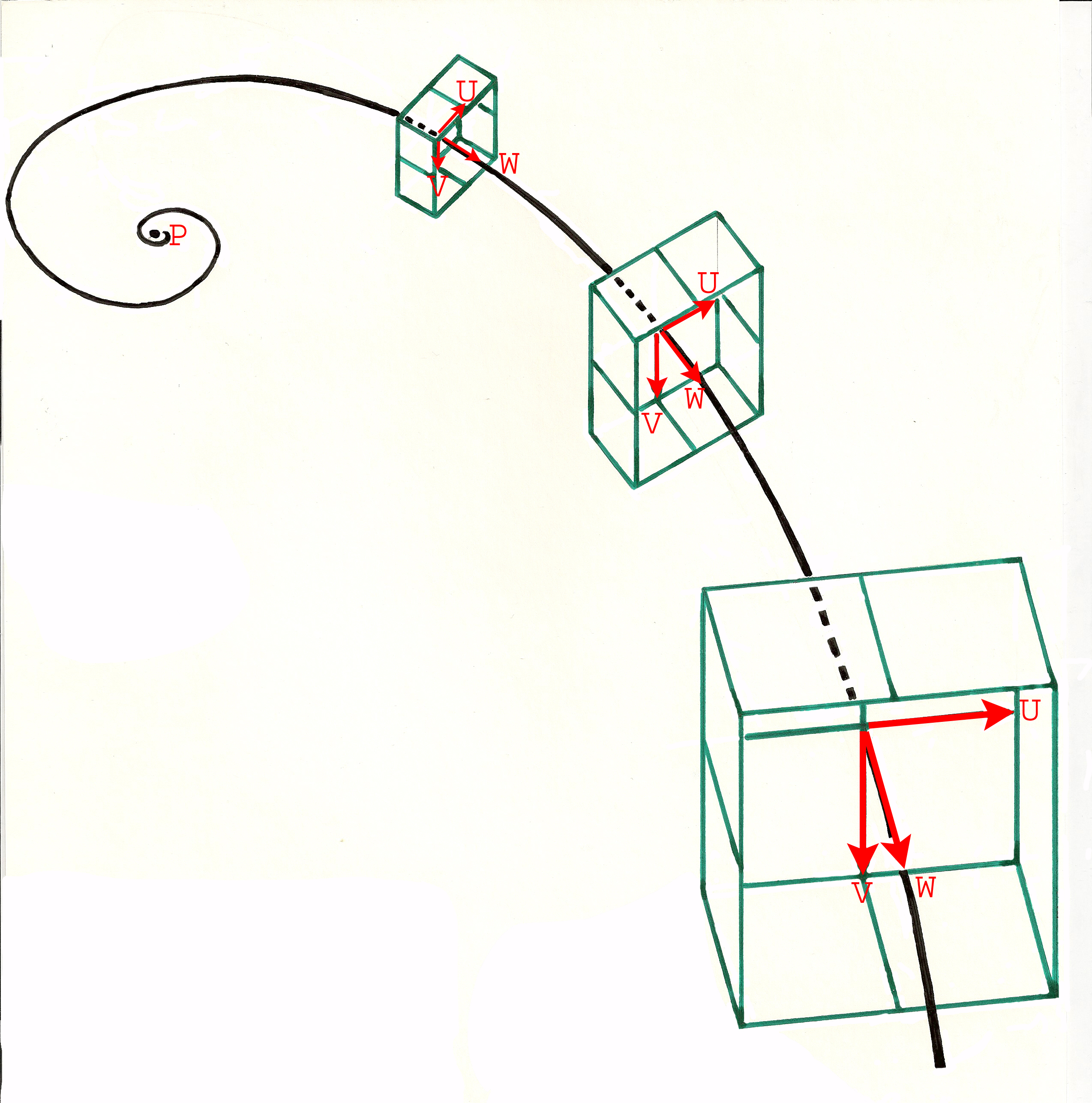
En chaque point du découpage non linéaire de l'axe curviligne est défini un espace vectoriel local, orthonormé ou non, mais dont les deux vecteurs U et V sont dans le plan perpendiculaire à l'axe et sont asservis au vecteur W défini par deux points consécutifs sur l'axe curviligne. Grâce aux remarquables propriétés qui découlent de la spirale logarithmique, tous les espaces vectoriels locaux, ainsi définis, sont homothétiques.
Tous les éléments d'objet décrits dans ces espaces locaux par des jeux de coordonnées identiques sont semblables, leurs proportions et surtout leurs angles sont identiques. Dans le cas des tiges Modular Plus, ce sont les sections transversales de forme rectangulaire et les 4 rainures qui sont définies dans les plans locaux U et V . Ces vecteurs U et V sont définis comme perpendiculaires au vecteur local W , défini par deux points consécutifs de même pas angulaire du découpage sur l'axe spirale, et leurs normes sont identiques. Par contre, la norme du vecteur W dépend de l'intervalle du découpage le long de l'axe, ce découpage n'étant pas linéaire mais à intervalles logarithmiques. Ces intervalles sont obtenus par les intersections de l'axe spirale avec des rayons-vecteurs issus du pôle progressant par des Pas Angulaires constants qui sont définis par un paramètre.
3.5.10. Tiges implantées dans un canal conique courbe.
Si la section locale de la tige possède une symétrie de révolution, ou si tous les points de la section transversale qui s'appuient sur l'os sont disposés sur un cercle, comme dans la tige Modular, il est très efficace et puissant de définir les points du dessin de la section en coordonnées polaires locales dans chaque plan de section. Les paramètres définissant ces points dans la Base de Paramètres sont communs à toutes les sections du découpage le long de la tige.
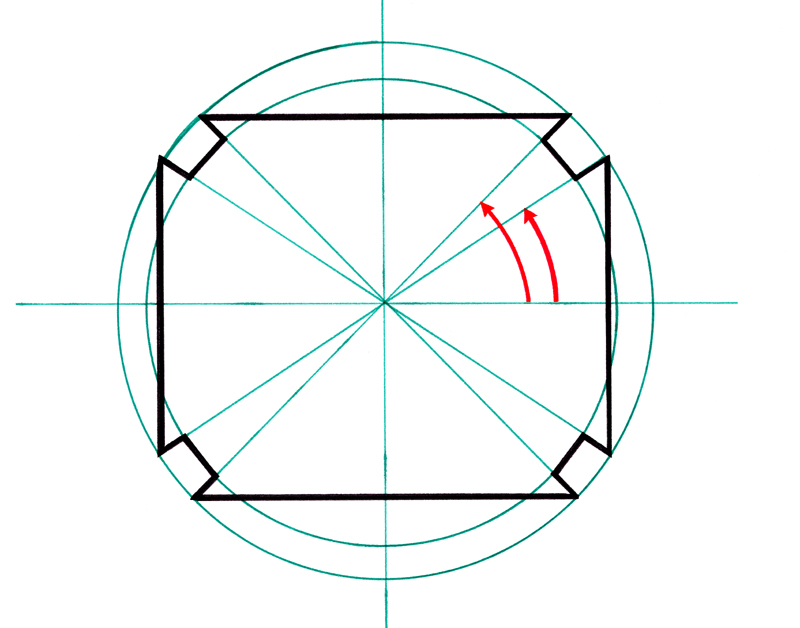
Quand les points de la section en cours sont calculés dans leur espace local, ils sont ensuite projetés dans l'espace général orthonormé et millimétrique destiné à alimenter les programmes de fraisage de la fabrication numérique. Les angles utilisés pour cette projection sont ceux obtenus à partir de l'orientation du vecteur local W délimité par deux points consécutifs du découpage de l'axe curviligne.
----
