3.1. La méthode des Facteurs de Croissance
3.1.1. Résumé
Pour satisfaire une grande diversité de patients avec une série de tiges fabriquées en série, il est nécessaire de prendre en compte les variations anatomiques ayant des causes largement indépendantes et des amplitudes très différentes, comme par exemple la longueur du fémur dépendant surtout de la taille du patient et le diamètre intérieur du canal médullaire qui varie surtout avec l’âge et l’activité du patient.
Pour obtenir ce résultat, les dimensions de la prothèse ( largeur, longueur, épaisseur ), les dimensions du col ( longueur, diamètre ), grandissent régulièrement d'une taille à la suivante, avec des valeurs définies indépendamment les unes des autres et en pourcentage pour chaque dimension.
Ce sont ces facteurs multiplicatifs ( analogues aux taux d'intérêt ) que j'ai appelés depuis 1981 " Facteurs de Croissance " ou " Growing Factors " ou " GF ".
3.1.2. Les Facteurs de Croissance
Les Facteurs de Croissance sont à la base de la méthode mathématique que j'ai spécialement développée en 1981 pour calculer les séries optimisées d’implants. Cette méthode permet en outre de calculer simultanément toutes les tailles de la série.
Pour satisfaire une grande diversité de patients avec des tiges fabriquées en série et non sur mesure, il est nécessaire de tenir compte de variations anatomiques, ayant des causes largement indépendantes, et des amplitudes très différentes. Par exemple, la longueur du fémur qui dépend surtout de la taille du patient et le diamètre intérieur du canal médullaire qui varie surtout avec l’activité et évolue avec l'âge.
La longueur, la largeur, l’épaisseur de la prothèse, la longueur et le diamètre du col, doivent grandir régulièrement d'une taille à la suivante pour obtenir ce résultat. Pour les séries de Tailles Optimisées, je fais varier chaque dimension, d'une taille à la suivante, avec des valeurs définies en pourcentage et indépendantes pour chaque dimension.
3.1.3. Exemples simplifiés de l'intérêt de la méthode
Pour simplifier l'explication, je préfère me restreindre aux longueurs, aux largeurs de tiges et aux longueurs de col ( d’autres dimensions étant moins démonstratives ).
Prenons pour exemple une série de seize tailles devant couvrir tous les patients, les tailles des patients s’échelonnant de 1,40 mètre à 2 mètres.
Donc du plus grand au plus petit, il y a une variation de 1,43, soit 43 %. Cette variation est à répartir sur les seize tailles de la série. Les largeurs de tiges correspondant aux diamètres du canal médullaire présentent, pour la même population de patients, des valeurs allant de 6mm à 30mm, soit une variation totale d’un facteur 5 donc de 400 %, également à répartir régulièrement sur les seize tailles.
Si le facteur de 1,43 de la longueur était également utilisé pour faire varier la largeur, on obtiendrait des tiges variant beaucoup trop peu en largeur ( par exemple de 10 à 14 mm ) et inutilisables tant pour les patients ayant un canal de 6 mm que pour les patients ayant un canal de 30 mm. Une solution vraiment satisfaisante de ce problème ne peut pas être obtenue en découpant l'intervalle de façon linéaire, entre la taille la plus grande et la taille la plus petite, de chaque dimension.
Exemple d'une série de tiges avant l'application de ma méthode. ( largeurs distales des tiges de Zweymüller première génération, 1979). largeur 10, 12.5, 15, 17.5, 20. Entre 10 et 12.5 la croissance est de 1,25 soit 25 %. Entre 17.5 et 20 la croissance n'est que de 1,14 soit 14.3 %.
Pour un patient dont le fémur aurait théoriquement nécessité une tige de 12 (non disponible ), on ne peut implanter qu'une taille 10. Le patient aura reçu une prothèse de 20 % trop petite pour son fémur! Il sera mal prothésé avec risque évident d'enfoncement ( ce cas est arrivé plusieurs fois en ma présence ).
Par contre pour un patient dont le fémur aurait nécessité une tige idéale de 17, c'est la taille 15 qui est disponible, donc seulement de 12 % trop petite pour son fémur. Ce patient sera " nettement " mieux équipé que celui de l'exemple précédent. Le fémur de ce patient, disposant d'un capital osseux plus important, aurait pu être élargi par râpage sans risque à 17.5, ce qui n'aurait pas pu être le cas du petit fémur de l'exemple précédent.
Cela montre, qu'avec un petit nombre de tailles distribuées linéairement, de grandes différences de conduite sont à tenir par l'Opérateur, d'un patient à un autre, et que les patients de petite taille reçoivent plus souvent des tailles inadaptées.
Il a existé sur le marché des prothèses dites " millimétriques " dont le grand nombre résolvait assez bien le problème des patients mais dont les écarts entre les très grandes tailles étaient inutilement rapprochés, nécessitant de plus un stock trop important.
J'ai donc recherché une modélisation mathématique permettant à tous les patients, du plus petit au plus grand, d'avoir des chances strictement égales de recevoir la taille la plus proche de la taille idéale, avec un taux d'imperfection et d'incertitude constant pour toutes les patients, et permettre à l'opérateur de conserver le même comportement pour le choix des tailles pour tous ses patients.
J'ai défini l'écart entre deux tailles successives de sorte que l'opérateur puisse toujours râper une demi-taille supplémentaire sans difficulté, et même un peu plus si nécessaire. C'est le principe essentiel du concept des Tailles Optimisées.
3.1.4. Choix des Facteurs de Croissance
J'ai d'abord, parmi toutes les dimensions d'un implant, défini quelles sont les dimensions qui doivent varier d'une taille à la suivante, dont les logiques sont indépendantes entre elles, et quelles sont les dimensions dont les logiques de variation sont liées.
Il m'a semblé suffisant de prévoir dans le procédé de calcul un maximum de 8 Facteurs de Croissance différents.
1. des facteurs importants comme ceux qui gèrent la largeur de la tige, la longueur de la zone d'ancrage dans l'os, la longueur de col et l'épaisseur antéro-postérieure,
2. des facteurs faisant varier le diamètre du col à la base du cône et l'amplitude de l'aileron trochantérien,
3. et éventuellement des facteurs dont l'utilité est secondaire, par exemple le diamètre des trous de suture et la taille des ogives distales, dont la variation n'a qu'un rôle esthétique mais qui donnent à la série sa belle impression de continuité.
Certains facteurs supplémentaires sont constitués par la combinaison linéaire de deux des facteurs précédents et serviront par exemple à l'échelonnement de la Fonction de l'Ogive Distale.
Chaque élément du Tableau des Facteurs de Croissance est obtenu avec les puissances successives du Facteur de Croissance choisi pour couvrir les 16 tailles prévues. La taille moyenne sert d'origine à l'échelonnement, tant vers les grandes tailles que vers les petites. Les tailles plus grandes que la taille moyenne reçoivent des puissances positives du Facteur de Croissance considéré, et les tailles plus petites que la taille moyenne reçoivent des puissances négatives.
Dans le logiciel, le nombre de facteurs et le nombre de tailles peut être étendu si nécessaire.
La description de détail de toute la géométrie de l'implant, commune à toutes les tailles de la série de prothèses, est rédigée sous forme de programme informatique. Le programme spécifique à une série d'implants comporte environ 4000 instructions. Aucun logiciel de dessin n'a été utilisé pour créer ces implants. Chaque détail géométrique a été formulé mathématiquement. Aucune approximation, aucun lissage ni générateur automatique de courbes n'ont été utilisés.
Dans mon système, c'est toute la série de tailles qui est calculée simultanément et le programme de description inclut toutes les relations entre les tailles successives, alors que pour les prothèses concurrentes, sans exception, la création est faite avec des logiciels de dessin assisté par ordinateur et seule une taille est élaborée à la fois, sans aucune relation formulée et calculée entre les tailles successives, et les dimensions sont définies et saisies manuellement.
3.1.5. Le système utilise certaines propriétés des espaces vectoriels
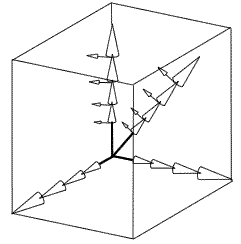
Au lieu de calculer une série de tailles tridimensionnelles dans un espace orthonormé ordinaire, dans lequel les vecteurs perpendiculaires entre eux, sur l'axe des X, des Y et des Z, ont la longueur de l'unité de mesure utilisée ( le millimètre par exemple ), je calcule la série de Tailles Optimisées dans un espace vectoriel de 8 dimensions pour chaque taille. Les 16 puissances de chaque facteur de croissance définissent seize vecteurs colinéaires de longueur différente. Les 8 facteurs de croissance peuvent être associés à 8 directions différentes de l'espace, certaines d'entre elles étant perpendiculaires entre elles et d'autres dans des directions indépendantes. De la sorte, la série de tailles prise pour exemple est calculée dans un espace vectoriel non orthonormé de 128 dimensions qui contiendra simultanément les coordonnées des 160 000 points de toutes les tailles de la série.
Les coordonnées obtenues sont stockées dans ce que j'ai nommé Base de Coordonnées ( différent de la Base de Paramètres). Comme tous les points des implants ont une position connue et sont numérotés, les coordonnées sont à tout moment consultables par tableaux pour procéder à des vérifications ou prélever des valeurs de contrôle pour la fabrication.
Les calculs une fois terminés, chaque taille est extraite séparément et projetée dans un espace orthonormé traditionnel pour permettre la production numérique. Mon logiciel Base de Transmission vers la production permet d'extraire uniquement les coordonnées utiles à la production au format, dans l'ordre et la disposition les plus favorables demandés par le fabricant. Ce dernier réalise l'adaptation spécifique à l'usinage numérique. Le descriptif de la transmission est unique et commun à toutes les tailles.
3.1.6. Choix fondamental de l'origine des coordonnées
Dans ce procédé, le choix de l'origine commune de l'espace vectoriel, donc l'origine des coordonnées, est fondamental.
En ce qui concerne les tiges fémorales, j'ai défini le centre de croissance et de coordonnées, à l'intersection de l'axe longitudinal du tiers proximal du fémur, de l'axe théorique défini par le centre de la tête fémorale et de la direction moyenne du col ( ceci pour une tige symétrique, les tiges non symétriques gauches et droites étant traitées un peu différemment ).
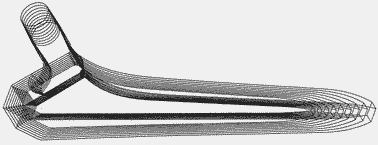
Dans un implant construit avec la méthode des Facteurs de Croissance, chaque détail de la structure est géré par un ou plusieurs Facteurs de Croissance prélevés parmi les 8 disponibles. Par exemple, les chanfreins à 45° des tiges SL Plus, situés tout le long de la zone d'ancrage, aux 4 coins de la section rectangulaire, sont également définis avec des Facteurs de Croissance et satisfont au micron près les principes de Jonction Conique et d'Emboîtement Ascendant.
La largeur de ces chanfreins augmente régulièrement depuis la pointe distale jusqu'à la partie proximale et varie pour chaque taille. En aucun cas, ce ne sont des chanfreins ou des arrondis d'arêtes de dimension constante introduits automatiquement par un logiciel graphique. La relation de ces chanfreins avec la forme correspondante des dents des râpes est importante et sera exposée séparément.
Contrairement à ce que certains ont prétendu de façon simpliste, la série de tiges SL Plus n'a pas été créée par homothétie ou agrandissement photographique, c'est à dire avec un facteur unique et constant dans toutes les directions de l'espace.
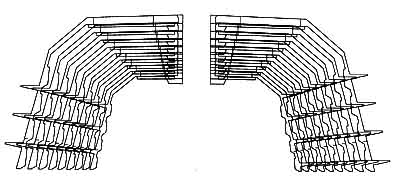
3.1.7. Comparaison entre la tige Zweymüller SL et la tige droite de Müller
Voici comme exemple la tige droite de Müller dessinée sans facteurs de croissance : la longueur du col métallique est constante pour toutes les tailles, la tête est fixe et l'Opérateur ne dispose d'aucun moyen de compensation des écarts résiduels de tension articulaire après durcissement du ciment.
Sur les variantes et les nombreuses copies des prothèses autoblocantes de Müller, disposant de têtes interchangeables, la longueur constante du col métallique était trop longue pour les petites tailles et trop courte pour les grandes.
Les cols courts, moyens et longs des têtes modulaires sont utilisés pour compenser l'absence de variation des cols et ne sont donc plus disponibles pour les dernières corrections de tension articulaire.
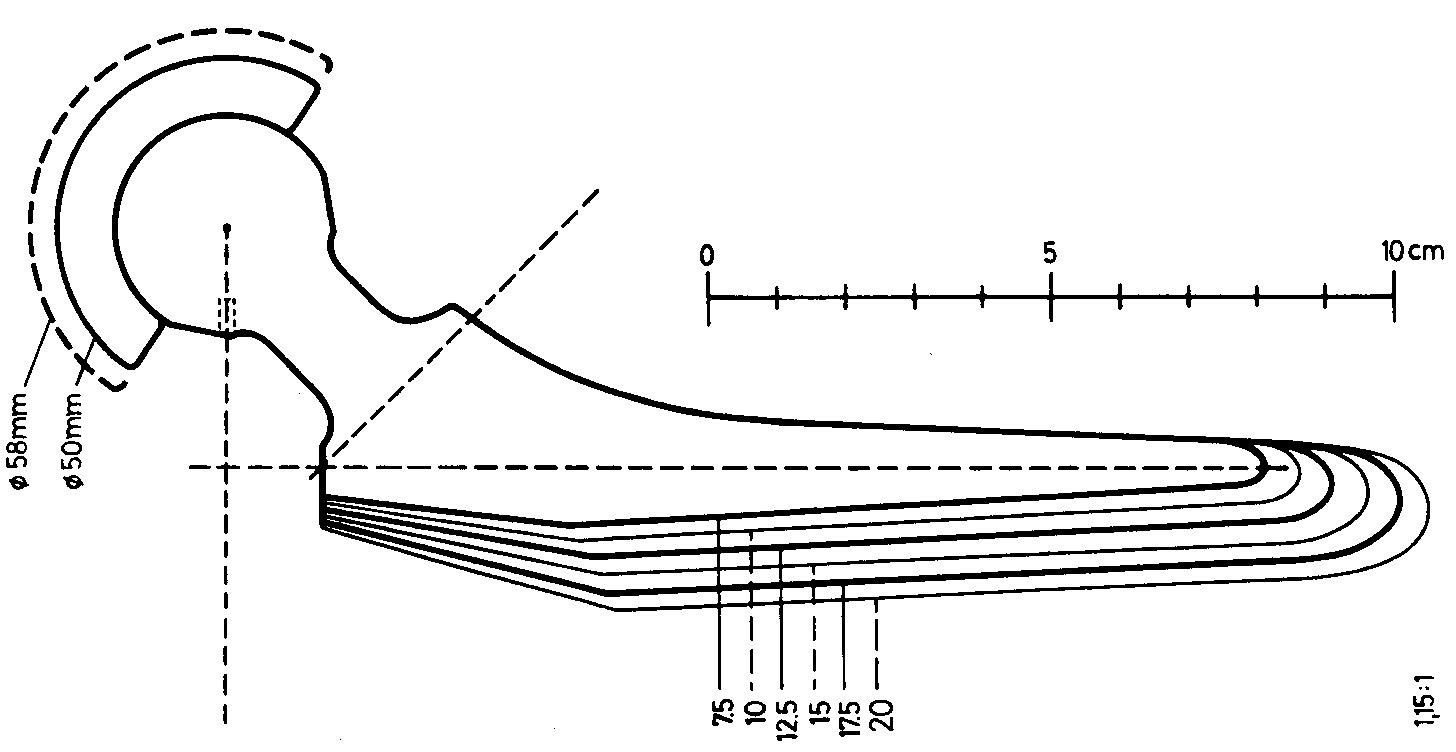
Dans mon concept, appliqué aux prothèses de Zweymüller, les cols métalliques varient régulièrement et la disponibilité des têtes à cols courts, moyens et longs, doit être réservée pour compenser les écarts résiduels de tension articulaire.
----
