3.6. Les Courbes de Transition
3.6.1. Résumé
Il s'agit d'un ensemble de différents procédés de modélisation permettant d'optimiser par exemple la transition entre la partie proximale d'une tige fémorale et la partie haute du col fémoral en remplacement des arcs de cercle traditionnels.
Selon la zone considérée sur les implants, la recherche de la meilleure résistance mécanique compte tenu du métal et de son traitement, les nécessités liées à la limitation de l'espace disponible dans les lits osseux, les précautions à prendre pour éviter les contacts préjudiciables entre des composants en mouvement, les modèles de Courbes de Transition peuvent être très différents.
Enfin la recherche de courbes de transition pourra être étendue progressivement dans le futur à la modélisation des trajectoires de plus en plus complexes des travées osseuses.
J'ai effectué plusieurs incursions dans ce domaine en introduisant des trajectoires non planes dans certains projets de prothèses conçues pour être au plus près de l'anatomie.
3.6.2. La quête de meilleures modélisations.
Dans mes quêtes successives pour rechercher les courbes de transition idéales entre la direction de l'axe d'une tige fémorale et la direction du col, j'ai eu l'occasion de mettre en œuvre plusieurs modélisations mathématiques.
Jusque là et quasiment sans exception en construction mécanique, on passait d'une direction à une autre en utilisant un arc de cercle pour éviter la fragilisation d'une pièce à l'endroit du changement de direction. Cela convient parfaitement tant qu'il n'y a aucun impératif supplémentaire sur le dessin de la pièce mécanique, comme par exemple des limitations de place ou de poids ou de conflit avec une autre pièce. Même en aéronautique, si une pièce n'est pas suffisamment solide, il suffit de la faire plus grosse et plus lourde !
Par contre, pour les implants orthopédiques, la place dans l'os du patient étant limitée, on peut difficilement implanter une taille plus grosse que sa cavité médullaire.
3.6.3. Les Courbes de Transition et la méthode des Eléments Finis
La méthode de l'analyse par " Eléments Finis " des contraintes subies par les pièces mécaniques est fréquemment utilisée pour tester les implants dessinés par les logiciels de CAO. J'ai pris connaissance de cette méthode en suivant les cours des Professeurs Lavaste et Landjerit aux Arts et Métiers de Paris.
Cette méthode permet de simuler les contraintes subies par une pièce mécanique et de mettre en évidence les zones où la pièce sera surchargée et risquera de se rompre. Ensuite, la pièce est corrigée ou redessinée, sans calculs, et on applique la méthode à nouveau pour savoir si les corrections étaient avantageuses. Par exemple, on agrandit un peu le rayon des arcs de cercle de transition. Il s'agit d'une méthode de validation a posteriori d'un dessin déjà terminé. La méthode nécessite d'importants moyens de calcul et, tout en étant informatisée, fait intervenir de nombreux paramètres parfaitement subjectifs définis approximativement par l'opérateur.
L'étude par la méthode des " éléments finis ", d'un objet tridimensionnel nécessite de découper cet objet en petits volumes élémentaires, par exemple des tétraèdres, dont les côtés ne sont ni très petits, ni infiniment petits, mais de dimensions " finies " connues, mesurables et calculables. Ce découpage en petits volumes élémentaires ( "discrétisation" ) est souvent automatisé par le logiciel, et dans ce cas le maillage obtenu est abondant, mais désordonné et obéit surtout à des choix de densité ou de dimensions. Par contre, il est aussi possible de définir manuellement les noeuds du maillage, ce qui est particulièrement laborieux. Seulement un minimum de points sont saisis et la précision des résultats est plus faible.
Souvent, on renonce au maillage tridimensionnel pour n'étudier l'objet qu'en coupe plane. On extrapole les résultats à la troisième dimension par déduction logique, mais en prenant le risque d'erreurs grossières. Un exemple typique de cette simplification excessive a été l'analyse comparative des tiges de Zweymüller par HUISKES. Cette procédure a occulté la troisième dimension qui est pourtant à l'origine de la supériorité clinique des tiges Zweymüller.
Ma philosophie est plutôt d'anticiper, par la réflexion et la théorie, les résultats que l'on obtiendrait de façon prévisible avec la méthode des éléments finis. Pour les différentes zones des implants, j'ai recherché des modélisations mathématiques favorables et programmables.
Cela permet de ne pas subir les trop fortes approximations de la méthode des éléments finis. Un contrôle par les éléments finis est toujours intéressant par la suite.
3.6.4. La chaînette
Dans une prothèse de hanche, la zone intertrochantérienne, entre le sommet proximal de la tige et le col est une zone où le métal est toujours sollicité en traction par les contraintes provenant de la tête. Il faut remarquer que les prothèses à tige intramédullaire diffèrent de la réalité de l'architecture du fémur naturel car le grand trochanter, qui était initialement lié au col naturel, n'est plus lié au col prothétique, et un petit liseré que j'attribue plutôt aux mouvements élastiques du grand trochanter qu'aux mouvements de la tige dans la diaphyse peut être observé. L'exception est l'exemple des anciennes tiges dites " isoélastiques " de Robert Mathys, où il a fallu relier le trochanter à la tige par une vis de traction pour tenter de compenser son hyperélasticité.
Une façon de modéliser cette région est d'imaginer ( sans le faire réellement ) dans cette zone une " discrétisation " par couches, c'est-à-dire par le découpage théorique de l'objet d'abord en couches successives à la façon des couches d'un oignon, et ensuite par le découpage de chaque couche par un maillage. Chaque couche considérée indépendamment se comporterait comme si elle était soumise à une traction à la façon d'une peau tendue, tout en restant en réalité adhérente à la masse métallique sous-jacente. De la sorte, chaque couche prendrait de façon idéale la forme de la " chaînette ". La " chaînette " ou caténoïde est la courbe prise naturellement par la chaînette d'un collier, d'une part du fait de la gravité sur chacun des maillons de masse constante, et d'autre part de la constance évidente de la tension en chaque point tout le long de la chaînette.

A cause de cette analogie, on appelle communément " courbe en chaînette ", la courbe plane décrite mathématiquement par le Cosinus Hyperbolique de la forme Y = ch X . avec: CH X = ( e^x + e^-x )/2 ou la forme développée en série que j'ai utilisée: CH X = 1 + X^2/2! +X^4/4! + X^6/6! + X^8/8! + X^10/10! + etc ...


3.6.5. Rencontre avec Gaudi... un siècle après
Récemment, en 1999, alors que la plupart de mes projets de prothèses étaient terminés, j'ai pris connaissance à Barcelone des étonnantes oeuvres de Antoni Gaudi ( 1852 - 1926 ). Ma satisfaction provenait de la grande analogie de sa démarche intellectuelle pour traiter les courbes de transition, avec celle que j'avais adoptée depuis 25 ans pour concevoir les courbes et surfaces de transition dans les implants. Depuis longtemps j'étais passionné par les familles de courbes passant progressivement des formes angulaires à des formes arrondies, que j'ai appelé ici Courbes de Transition.
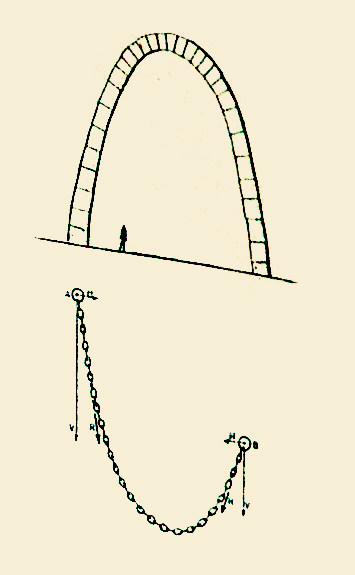
Le célèbre architecte de Barcelone, Antoni Gaudi, a eu la fabuleuse intuition de dessiner les plans de la cathédrale de Barcelone et les voûtes de nombreux bâtiments en reprenant exactement les formes inversées de chaînette prises naturellement par ses maquettes constituées de fines cordelettes suspendues au plafond de son atelier.




{{ $3266_gaudi_guellcrypte_dan.jpg := $3266_gaudi_guellcrypte_dan.jpg.Resize "100x" }} essai 92
essai 18 #{{ /3266_gaudi_guellcrypte_dan.jpg := /3266_gaudi_guellcrypte_dan.jpg.resize "100x" }} #

#

#

essai 14 resize dehors 15 600x 16 resize 600x 17 resize "600"
#

essai 13 r, 12 R
#

essai 11
#

essai 10
#

essai 9 ,8
#

essai 7
#

essai 6
#

#{{ /3266_gaudi_guellcrypte_dan.jpg := /3266_gaudi_guellcrypte_dan.jpg.Resize "100x" }}
>La crypte réalisée en maçonnerie d'après la maquette filaire
3.6.6. Gaudi chercheur en Géométrie
Dans l'atelier à côté de son bureau, Gaudi a développé un véritable programme de recherche sur les aspects de la géométrie qui pouvaient être importants pour son travail d'Architecte ... Il se concentrait sur la quête expérimentale de solutions géométriques optimales qu'il pourrait appliquer à ses projets. Courbures, surfaces et transformations ne l'intéressaient que si il pouvait les appliquer dans ses constructions. ... Il créa un univers géométrique au service de sa propre créativité. ( Claudi Alsina i Català, Mark Burry, Gaudi Unseen, Jovis Berlin. )
Si les autres bâtisseurs de cathédrales avaient eu les intuitions de Gaudi, des centaines d'édifices ne seraient actuellement pas des tas de ruines.
Pour plusieurs familles d'implants, j'ai choisi cette modélisation par chaînette de la zone où le métal est sollicité en traction, en introduisant les coordonnées, calculées au préalable par la fonction Cosinus Hyperbolique, dans les paramètres décrivant la Courbe de Transition intertrochantérienne jusqu'à la base de la jonction conique avec la tête.


3.6.7. La courbe de transition hyperbolique

Pour modéliser la transition entre la zone d'ancrage et le col cylindrique de la tige AlloClassic ( 1984 ), ne voulant pas appliquer une courbe de transition en arc de cercle que je trouvais trop encombrante, j'ai recherché une courbe quittant très progressivement la zone d'ancrage et dont la courbure variait régulièrement pour atteindre tangentiellement la base du col cylindrique.
Mon application de la transition hyperbolique à la famille des tiges AlloClassic a fait l'objet de mon brevet .... ( 6.2.6. ).
Grâce à sa courbe de transition en forme d'arc d'hyperbole, la tige AlloClassic entrait très rarement en conflit avec le calcar au voisinage de la coupe du col. Cette forme a été critiquée car le remplissage et le contact avec le lit osseux en cette région ne semblait pas suffisants aux yeux de certains, du moins sur les radios de face.
Grâce à l'Ancrage Géométrique, la tige AlloClassic est pourtant suffisamment stabilisée par sa zone d'ancrage, et j'estime aujourd'hui qu'il n'était pas indispensable que le remplissage métaphysaire soit plus complet. Il était statistiquement très intéressant, pour l'exploitation correcte de la Réserve d'Impaction, de rendre rares les conflits qui auraient empêché 4 ou 5 millimètres d'impaction supplémentaire.
3.6.8. Les courbes de transition exponentielles
Radiologiquement, la tige AlloClassic restant parfois sans contact apparent avec le calcar, lors de la création de la tige SL Plus, il m'a été demandé d'augmenter le remplissage de la zone du calcar.
Pour la tige SL Plus, j'ai adopté une modélisation mathématique de la courbe de transition dont la variation du rayon de courbure le long de l'arc de transition pouvait être paramétrée plus aisément, alors que pour le modèle hyperbolique de la tige AlloClassic, la courbure maximale était toujours à la base du col cylindrique.
La modélisation par une portion de courbe exponentielle définie dans un système de coordonnées locales non orthonormé, ( voir 4.3.2. ), a pour avantage d'avoir une tangence parfaite avec la zone d'ancrage en son point de départ et permet de satisfaire ma Loi des Dérivées Positives et continues.
Cette modélisation permet également de paramétrer en continu l'angle de la tangente à la courbe au point d'arrivée à la base du cône de jonction. Cette modélisation remplace complètement la partie cylindrique du col. En pratique, les paramètres de cette courbe sont calculés automatiquement pour chaque taille par un algorithme par itérations successives.
3.6.9. La méthode des tirs de missiles dans le plan
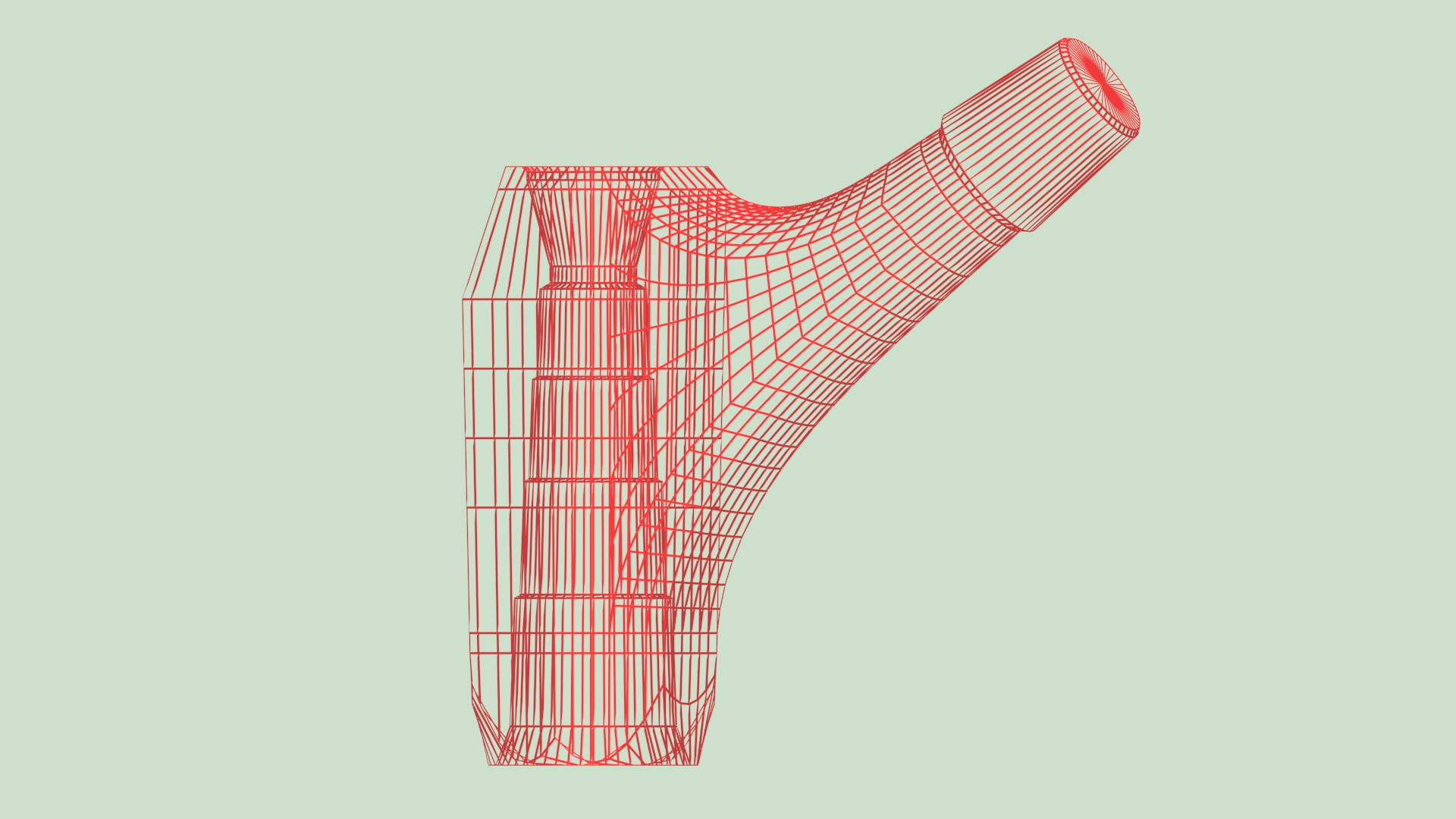
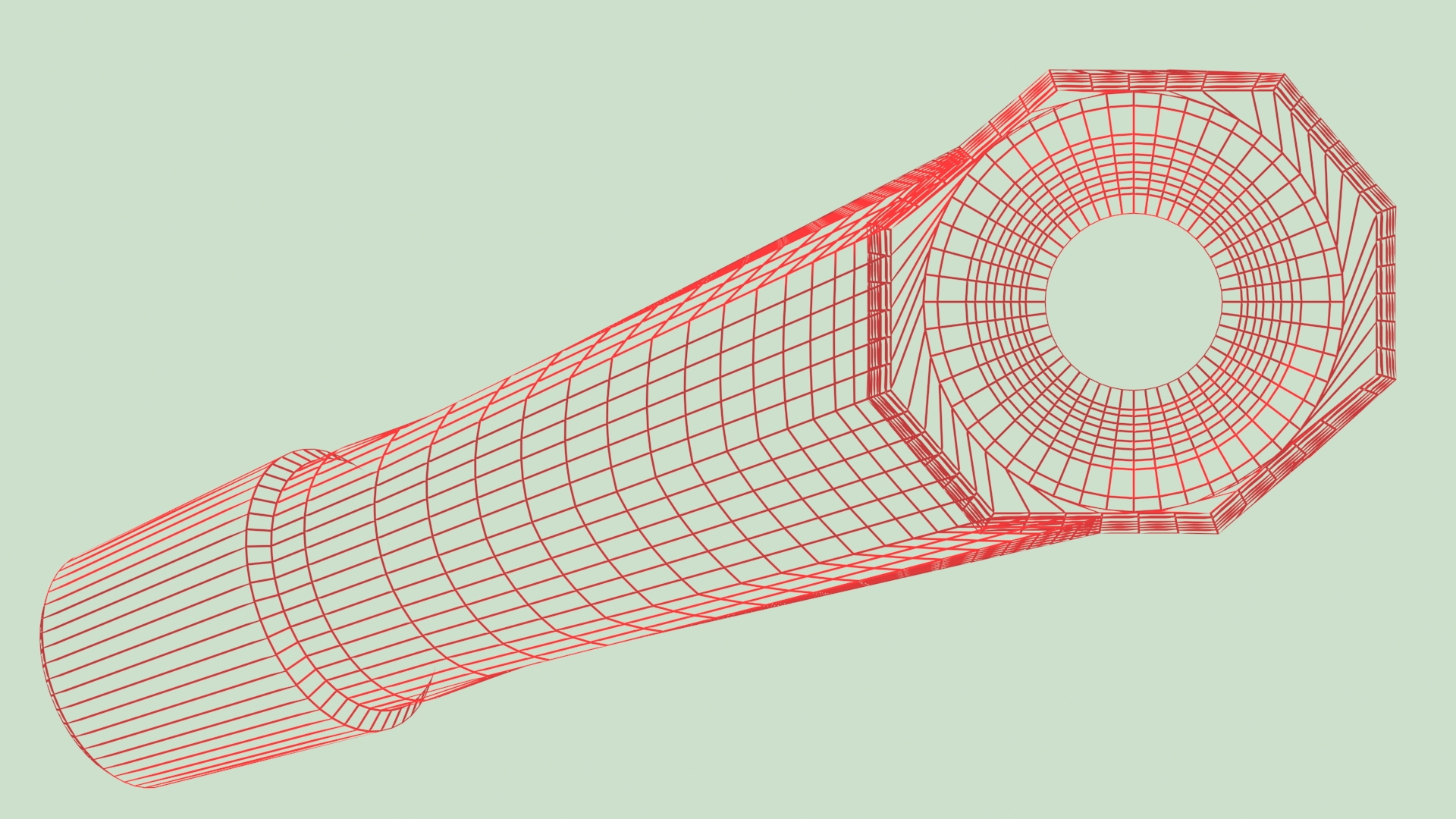
Pour la modélisation des pièces proximales du système Modular Plus, j'ai appliqué une méthode de calcul automatique. La symétrie gauche-droite de ces pièces permettait de décrire chaque courbe reliant la base de la pièce proximale à la base du cône de jonction, dans un plan vertical. La surface reliant la partie médiale de la base de la pièce à la moitié inférieure de la base du cône est composée de 24 courbes calculées successivement.
3.6.10. La méthode des tirs de missiles en trois dimensions
Pour la modélisation des pièces proximales non symétriques gauche-droit du projet ANA.NOVA, il n'était plus possible de conserver les courbes de transition planes. Le nouveau concept de décalage antérieur de l'axe du col, rapprochant encore l'implant de l'anatomie réelle de la partie proximale du fémur, nécessitait de raccorder la tige et le col par des courbes de transition tridimensionnelles.
Cette méthode réalise une simulation automatique des lignes d'orientation des composantes cristallines de l'os cortical et de l'orientation des travées osseuses de l'os spongieux, proche de l'orientation des contraintes réelles.
La génération de ces courbes de transition est une modélisation analogue aux trajectoires des missiles à tête chercheuse poursuivant une cible mobile, ne restant pas dans le plan vertical du lancement.
Pour être un peu plus explicite, le parcours partant de la tige vers la base du cône est divisé en un certain nombre de segments. Par une itération automatique de l'algorithme, les segments successifs sont partiellement déviés en 3D en direction de la cible, pour aboutir au dernier segment à se trouver aligné avec le segment ciblé sur la périphérie du cône, et ceci sur 24 trajectoires différents en 3D.

----
Chapitre suivant: 4. Procédés spécifiques aux tiges fémorales
