4.2. La Forme de Base Pyramidale
4.2.1. Résumé
Les tiges fémorales à Ancrage Géométrique doivent d'abord être aptes à constituer une véritable jonction conique avec le fourreau osseux rectifié.
Les tiges sans ciment AlloClassic et SL Plus, sont construites à partir d'une forme de départ de pyramide à base rectangulaire, qui appartient géométriquement à la famille des cônes. Cette forme de zone d'ancrage permettra d'obtenir la fixation dans l'os par jonction de type conique.
Cette Forme de Base Pyramidale subira des modifications de faible amplitude avec les Corrections d'Epaisseur et constituera par la suite le premier terme du Polynôme du Calcar.
4.2.2. L'origine de la Forme de Base Pyramidale
Dans l'heure qui a suivi une participation à une opération à Nice, en Mars 1984, j'ai brusquement eu la compréhension du défaut tridimensionnel des tiges de Zweymüller de première génération, et j'ai immédiatement dessiné le schéma théorique que j'aurais souhaité pour ces tiges. Si ces tiges avaient possédé la propriété d'une pyramide, les instabilités peropératoires que je venais d'observer n'auraient pas eu lieu.
Dès les jours suivants, l'idée de la nécessité d'une refonte des tiges de Zweymüller sur des bases strictement géométriques m'est apparue nécessaire. Cette idée a été confortée par les problèmes d'échelonnement des tailles que j'avais constaté au cours des trois années précédentes.
4.2.3. Application aux tiges que j'ai conçues par la suite
J'ai commencé à réfléchir, a étudier les améliorations que je comptais proposer un jour pour la rénovation du système de première génération et à élaborer les moyens mathématiques et informatiques pour les mettre en oeuvre.
Pour les futures tiges AlloClassic sur lesquelles j'ai travaillé chez moi tout au long de l'année 1984, j'ai fait correspondre exactement la zone d'ancrage à la forme de la pyramide de base.
Au cours des huit années qui ont suivi, j'ai complété et affiné cette forme pyramidale simple par les fonctions additives du Polynôme du Calcar. J'ai appliqué cette forme plus évoluée aux tiges SL Plus.
4.2.4. Le Centre de Croissance
Le squelette de la tige SL Plus a la forme d'un tronc de pyramide limité en proximal par un contour rectangulaire situé à l'origine des coordonnées et simultanément à l'intersection de l'axe longitudinal avec l'axe oblique du col de la prothèse. L'origine des coordonnées a une grande importance dans la conception des prothèses que j'ai crées car c'est le point de départ des différents vecteurs de base qui vont définir l'expansion de l'implant en fonction des tailles dans toutes les directions de l'espace 3D, un peu comme on l'imagine poétiquement pour le " Big-Bang " mais de plus avec des " vitesses " indépendantes dans chaque direction. J'ai appelé ce point le Centre de Croissance.
4.2.5. Auparavant ni forme de base ni Centre de Croissance
Aucune forme de base, quelle qu'elle soit n'est utilisée pour la plupart des implants du marché dessinés et sans définition d'un Centre de Croissance pour définir les différentes tailles. Chaque taille est dessinée indépendamment des autres.
Le point d'intersection entre l'axe longitudinal, quand il existe, et l'axe du col est rarement pris en compte et n'est pas considéré comme un point important de la construction.
Même lorsque je participais à la rédaction des Normes européennes sur les prothèses, il ne m'a pas été possible de faire définir une relation logique ni entre l'axe longitudinal et la tige elle-même, ni entre l'axe du col et son intersection avec l'axe longitudinal.
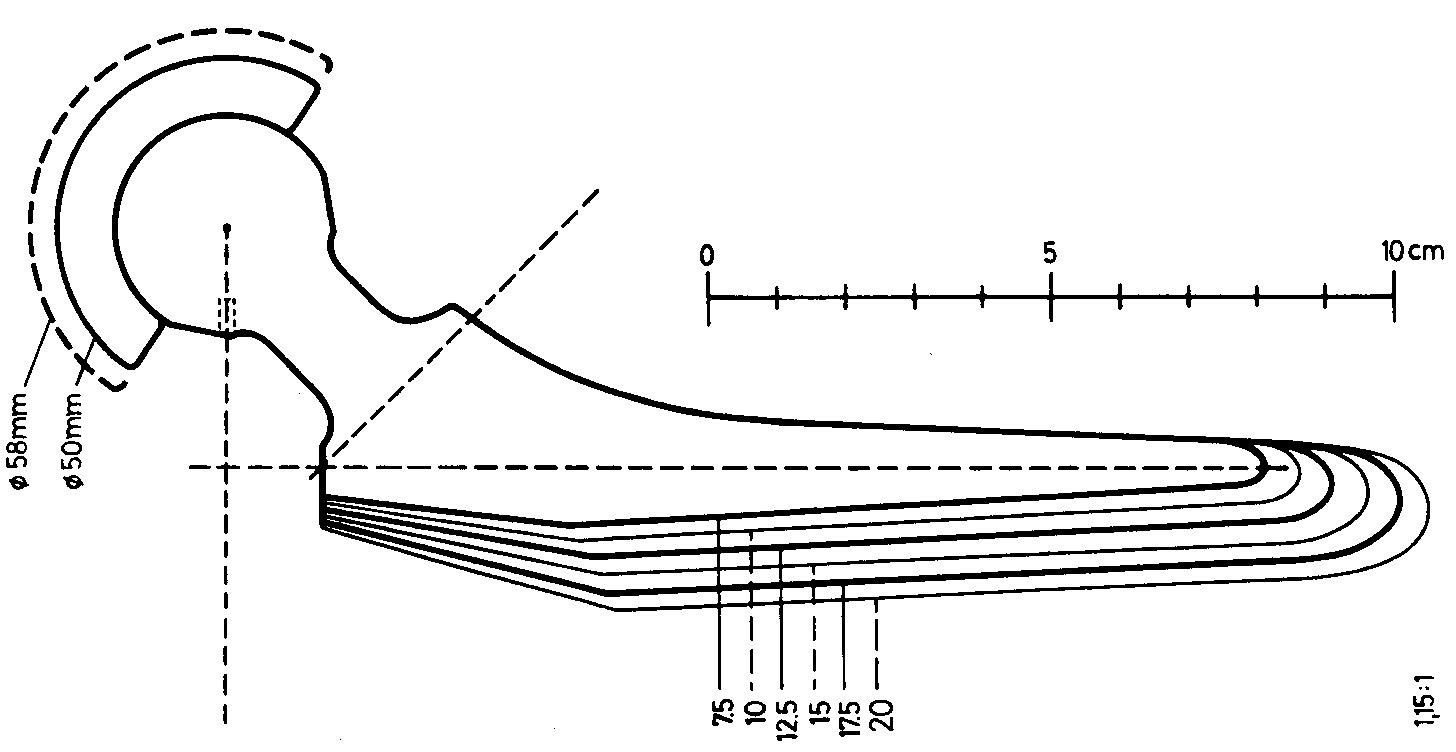
4.2.6. Définition de la Forme de Base Pyramidale
La Forme de Base Pyramidale est définie d'abord par la longueur de la zone d'ancrage choisie pour la taille moyenne de la série. Ce vecteur sera normé, dans la direction de l'axe longitudinal, par le Facteur de Croissance propre à chaque taille.
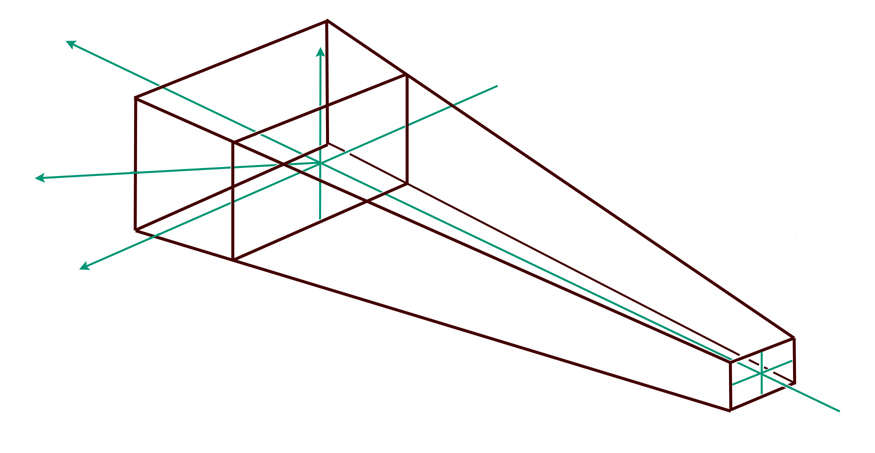
Ensuite, la largeur proximale est définie par un vecteur perpendiculaire partant également du Centre de Croissance et adaptée à chaque taille par le Facteur de Croissance des largeurs.
L'épaisseur de la section proximale de la zone d'ancrage de la taille moyenne est obtenue par un Facteur de Forme appliqué à la largeur. J'obtiens ainsi la forme du rectangle de la section. Cette épaisseur n'est pas saisie comme donnée définie en millimètres. Elle est calculée par le programme.
Suite à l'application de la méthode des Corrections d'Epaisseur, la forme de cette section variera légèrement et de façon continue, de la section distale de la taille la plus petite de la série jusqu'à la section proximale de la taille la plus grande. En conséquence, les tiges de grande taille sont plutôt aplaties et les tiges de petite taille ont une section qui se rapproche du carré.
Toutes les Formes de Base Pyramidales de toutes les tailles satisfont le Principe de l'Emboîtement Ascendant.
Seul l'angle principal de face de la Forme de Base Pyramidale est saisi sous forme d'une donnée. Les angles entre les faces antérieure et postérieure sont calculés automatiquement par le logiciel. Leur résultat, qu'il est inutile de connaître au départ, est la conséquence géométrique du Facteur de Forme et du traitement par la Méthode des Corrections d'Epaisseur.
Pour les tiges calculées avec le Polynôme du Calcar, les Fonctions de Fixation et de Séparation apportent à la Forme de Base Pyramidale des variations légères mais continues tout le long de la tige, ces angles ne sont ni constants ni mesurables sur l'implant.
