4.8. Les Corrections d'Epaisseur
4.8.1. Résumé
Dès l'origine, la zone d'ancrage des tiges de Zweymüller des trois générations a des sections rectangulaires.
Si les proportions du rectangle de la section étaient conservées identiques pour toute la série de tiges AlloClassic et SL Plus, le haut de la tige de taille 12 serait monstrueusement épais et inutilement rigide et par contre la pointe distale de la tige de taille 1 aurait été ridiculement mince et aurait rendu les tiges de très petite taille trop fragiles.
Pour éliminer ce problème, j'ai développé une méthode mathématique permettant de modifier en continu les épaisseurs de toutes les tailles à tous les niveaux des Pyramides de Base. La méthode amincit l'épaisseur du haut de la taille 12, et épaissit la pointe de la plus petite taille pour le rapprocher d'une section carrée, qui donne la meilleure résistance mécanique pour un diamètre donné.
Cette correction d'épaisseur permet de respecter les méthodes de l'Emboîtement Ascendant et des Tailles Optimisées et l'expression " toutes les tiges de la série semblent être extraites d'un même bloc métallique unique " reste vraie.
4.8.2. Application des Corrections d'Epaisseur aux tiges de section rectangulaire
Il aurait été facile de réaliser la série de tiges SL de 1984 en conservant des proportions constantes des zones d'ancrage pour toutes les tailles.
Certains ont pu croire que les tiges SL croissaient de façon homothétique, ce qui est une erreur. Si l'on conservait des proportions constantes, avec le même facteur de forme pour la section transversale pour toutes les tailles, et tout le long de chaque tige, en prenant le facteur de forme de la taille moyenne qui s'est avéré convenable, les tiges de petite taille, comme par exemple les tailles 1 et 2, deviendraient extrêmement fragiles à cause de la section rectangulaire très aplatie.
Il en est de même pour les grandes tailles 11 et 12. Si le facteur de forme de leur section avait été maintenu identique à celui du milieu de la taille moyenne, ces tiges deviendraient monstrueuses en volume global et de plus auraient perdu le peu d'élasticité que le Titane permet.
Ces problèmes ne s'étaient pas posés aux Auteurs de la Zweymüller première génération. Toutes les tiges avaient une épaisseur constante d'environ 9mm, de la tige “10” à la tige “17.5”, comme si elles avaient toutes été découpées dans la même plaque de tôle de Titane de 9mm d'épaisseur. Bien sûr cette épaisseur diminuait un peu le long de la tige, d'ailleurs avec des angles aléatoires, ni définis ni calculés.
Ces réflexions ont été confirmées sept ans plus tard par l'étude comparative des résistances mécaniques des tiges Spotorno et Zweymüller SL par Manfred Semlitsch, Sulzer, 1991. Les différences mises en évidence dans cette étude étaient en partie dues à la méthode de la mesure "en torsion", qui est obtenue par la fixation inclinée de 10 degrés en antéro-postérieur de la tige dans le montage expérimental.
4.8.3. Les Corrections d'Epaisseur sont compatibles avec le Principe d'Emboîtement Ascendant
Pour satisfaire le principe d'Emboîtement Ascendant, toutes les tailles de tiges SL, sont extraites par calcul, à des niveaux différents et avec des longueurs différentes, dans une même et unique enveloppe géométrique schématisant une barre virtuelle de Titane dans laquelle seraient découpées toutes les tiges.
4.8.4. Aspect mathématique des Corrections d'Epaisseur
Les tiges SL, puis par la suite SL Plus, possèdent, avant l'application des calculs pour la Correction d'Epaisseurs, un facteur de forme constant.
Ce facteur de forme résulte d'une décision de conception et s'applique au niveau moyen de la taille moyenne de la série de tiges. C'est un élément de la base de paramètres.
J'utilise ici la définition suivante : rapport compris entre 0 et 1 entre le petit côté et le grand côté d'un rectangle, et plus généralement du rectangle exinscrit autour d'un contour de forme quelconque, le grand côté étant dans la direction du plus grand diamètre.
L'angle de la “conicité” antéro-postérieure n'est pas une valeur définie en tant que Donnée.
De plus, pour les tiges SL-plus et SLR-plus, l'angle n'est pas constant et varie un peu tout le long de la tige du fait d’une fraction du “ Polynôme du Calcar ” proportionnelle au Facteur de Forme à chaque niveau, appliqué également aux faces antérieure et postérieure. Cette variation d'angle est visible à l'oeil nu pour les tiges SLR-Plus et Holz-Zacher par exemple.
Certains rédacteurs de marketing ont indiqué des valeurs angulaires fantaisistes, sans me demander la moindre information.(citations) Je ne connais pas moi-même la valeur exacte de cet angle car il provient d'un calcul informatique automatique qui prend en compte de nombreux paramètres de la tige.
4.8.5. Les Corrections d'Epaisseur traitent la Forme de Base Pyramidale
Les calculs de Corrections d'Epaisseurs sont appliqués à la Forme de Base Pyramidale ayant un Facteur de Forme constant, pour permettre de s'écarter, modérément et progressivement, de ces formes de base afin que la section à la pointe distale de la plus petite taille de la série soit pratiquement carrée, et que la section proximale de la plus grande taille soit relativement aplatie.
De la sorte, les très petites tailles de tiges auront la meilleure résistance mécanique possible pour de petites dimensions de Titane (article du Dr. Semlitsch) et les très grandes tailles seront moins colossales d'autant que peu de problèmes de résistance mécanique sont à redouter.
4.8.6. Exemple de formulation paramétrée des Corrections d'Epaisseur
La traduction en langage clair de la formulation codée permet l'identification des paramètres utilisés dans le calcul des corrections d'épaisseur :
Boucle sur 16 tailles
epaisseur1=facteur de forme x .5 x ( facteur de croissance1,Taille1 )
epaisseur2 = facteur de forme x .5 x ( facteur de croissance1,TailleReference) + facteur de forme x ( Facteur de croissance2,TailleReference ) x tangente demi angle face
correcteur1 = correction proximale x ( epaisseur2-facteur de forme x ( demi largeur proximale, TailleEncours ) ) / ( epaisseur2 - epaisseur1 )
correcteur2 = correction proximale x ( facteur de forme x (demie largeur proximale,TailleEncours ) - epaisseur1 ) / ( epaisseur2 - epaisseur1 )
demi épaisseur proximale corrigée = ( demi largeur proximale,TailleEncours ) x facteur de forme + ( demi correcteur1 + demi correcteur2 )
correcteur3 = correction proximale x [ epaisseur2 - facteur de forme x ( demi largeur distale, TailleEncours) ] /[ epaisseur2-epaisseur1 ]
correcteur4 = correction distale x ( facteur de forme x ( demi largeur distale, TailleEncours) ) - epaisseur1 / ( epaisseur2 - epaisseur1 )
demie épaisseur distale=largeur distale x facteur de forme+demi correcteur3 + demi correcteur4
4.8.7. Le résultat fournit le premier terme du Polynôme du Calcar
Après application des calculs des Corrections d'Epaisseur à toutes les tiges de la série, on obtient la Forme de Base Pyramidale des zones d'ancrage.
Ce sont ces contours qui vont constituer le premier terme du Polynôme de Calcar de la tige SL Plus. La zone d'ancrage des tiges AlloClassic était uniquement constituée par les formes précédemment obtenues.
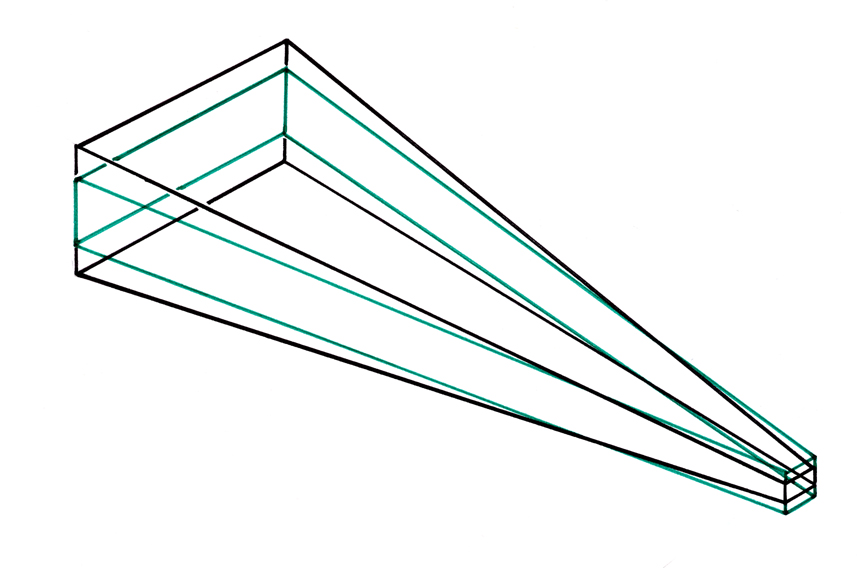
Figure : Représentation schématique de la barre de Titane unique traitée par les Corrections d'Epaisseur.
----
