3.5. Der Logarithmische Spirale Raum
3.5.1. Zusammenfassung
Zur Entwicklung gekrümmter Implante, die sich besser als Schäfte mit geradliniger Achse in ebenfalls gekrümmte Diaphysen einfügen, jedoch alle Prinzipien der Geometrischen Verankerung erfüllen, führte ich eine mathematische Studie durch, aus der eine einzigartige Schlußfolgerung resultierte: nur in einem gekrümmten Logarithmischer Spirale Raum berechnete Schäfte können diese Anforderung erfüllen.
Da ich über keine frühere Quelle verfügte, entwickelte ich zur Beschreibung dieser Implantate eine neue mathematische Methode.
Zwei Familien gekrümmter Schäfte wurden im gekrümmten Raum in Logaritmischer Spirale entworfen
Modular-Plus Schäfte für tiefe Reoperationen
und die Schaftfamilie des Anantomica.Nova-Projektes, die die ganze Bandbreite umfasst: Erstoperation, Reoperation und tiefe Reoperation.
Außerdem konnte ich die Entwicklung zur Konzeption des “Umgekehrten Spiralräumers”, der zur Implantation der gekrümmten Modular-Plus-Schäfte für tiefe Reoperationen mit geometrischer Verankerung dient, weiter vorantreiben. Die Beschreibung dieses äußerst originellen Instruments wird weiter unten ausgeführt.
3.5.2. Geometrische Verankerung und gekrümmte Implantate
Implantate, die alle Eigenschaften der Geometrischen Verankerung besaßen, konnten scheinbar nur mit geradlinigen Hauptachsen verwirklicht werden. Ich fragte mich, ob es möglich sei, die Bedingungen der Geometrischen Verankerung mit gekrümmten Schäften zu erfüllen und kam zu folgenden Beobachtungen:
3.5.3. Die krummlinige Achse als Kreisbogen ist für die geometrische Verankerung ungeeignet
Ein Implantat, dessen krummlinige Achse und dessen Umrisse Kreisabschnitte wären, erfüllt aus mathematischer Sicht niemals die Prinzipien der Geometrischen Verankerung. Bei jedem Versuch, ein Implantat mit einer krummlinigen kreisförmigen Achse zu schaffen, würden zu ungenaue Näherungswerte entstehen. Das Prinzip der konischen Kupplung im Knochen wäre nicht erfüllt.
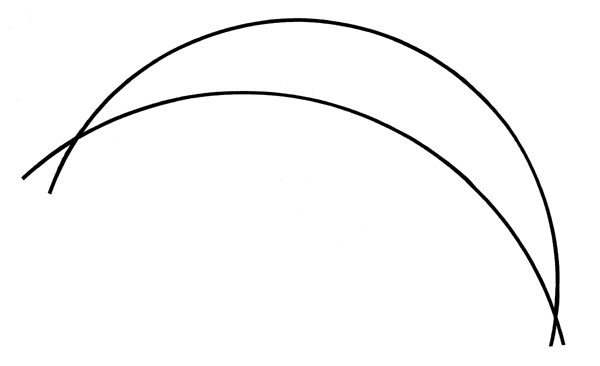
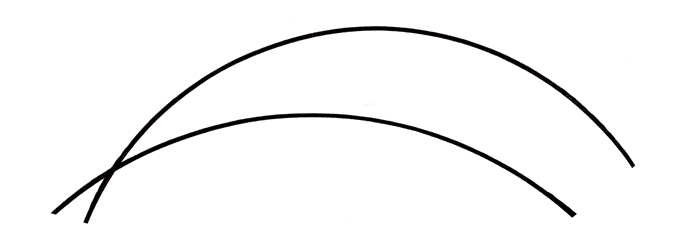
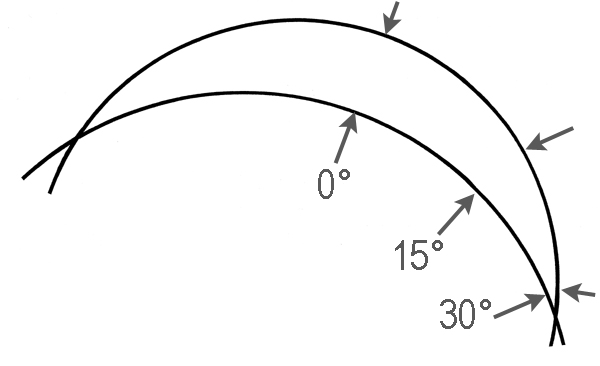
Versucht man eine konische Kupplung mit krummliniger Kreisachse in ein Schema zu bringen, indem man den Schaftumriss durch zwei Kreisbogen darstellt, die zwei Schnittstellen bilden, ist eindeutig zu erkennen, dass der Tangentenwinkel in zwei gegenüberliegenden Punkten auf den beiden Kreisen in keinem Bereich dieser Kreise konstant bleibt.
An den beiden Schnittstellen ist dieser Winkel maximal, während, wenn man sich von einem Schnittpunkt entfernt, die Kreise allmählich parallel werden und an der zweiten Schnittstelle schließlich sogar zusammentreffen. Man kann sich unschwer vorstellen, dass selbst das Hinzufügen der dritten Dimension zu dieser schematischen Geometrie nicht die Herstellung irgendeiner gekrümmten konischen Kupplung ermöglicht.
3.5.4. Die Logarithmische Spirale
Meines Wissens gibt es für diese Problem eine einzige mathematische Lösung, die durch die logarithmische Spirale geliefert wird. Diese besitzt die Eigenschaft, entlang der gesamten Krümmung einen konstanten Winkel zu bilden, und zwar zwischen der Tangente in einem Punkt der Spirale und dem Strahlenvektor, der diesen Punkt mit dem asymptotischen Pol dieser Spirale verbindet.
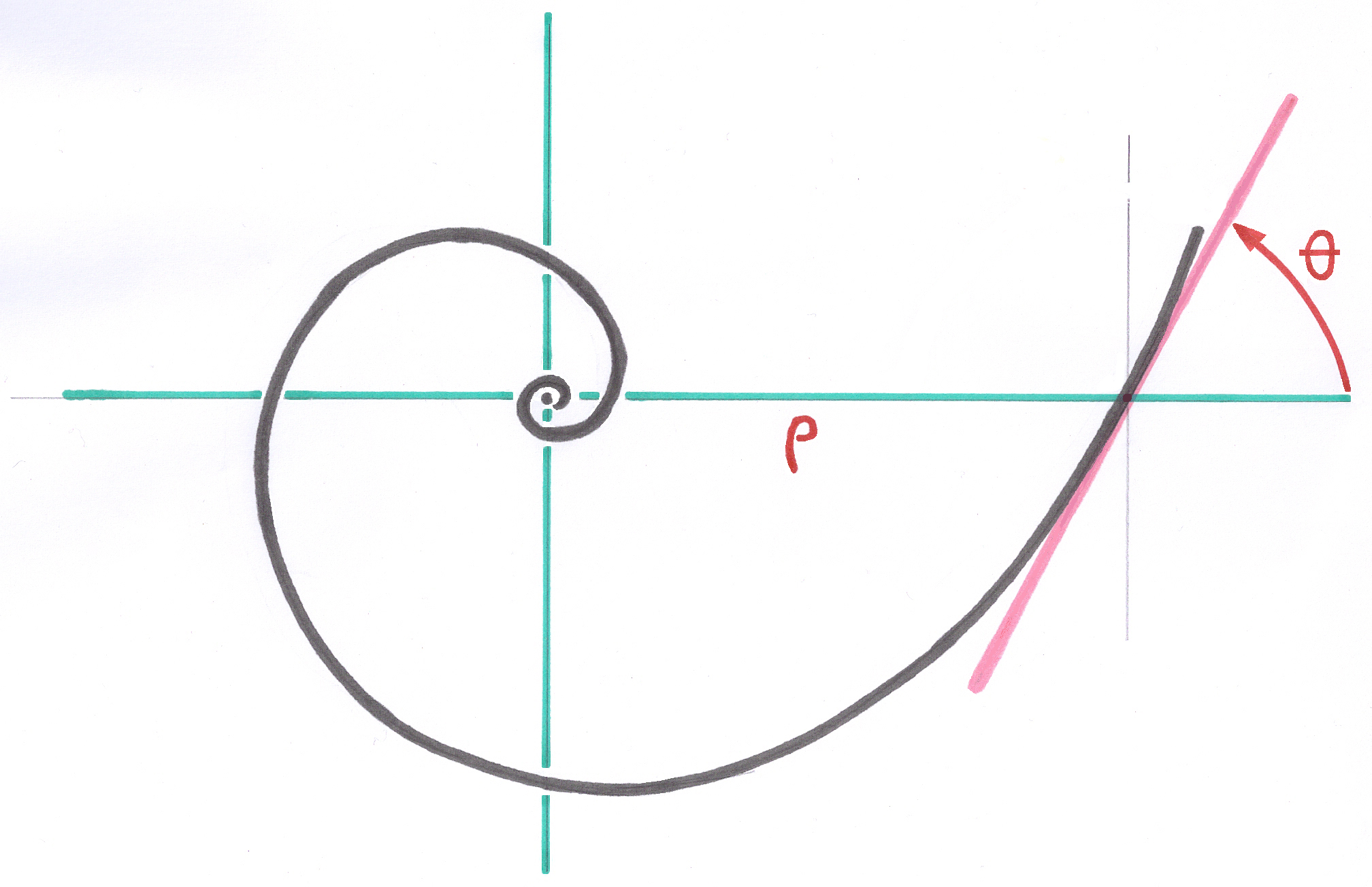
Die vielfachen graphischen mehr oder weniger groben Näherungen der Spiralen, die aufeinanderfolgende und wachsende Kreisbögen verwenden, und die man in allen Artikeln der Fachliteratur und im Internet unter dem Wort ‘Spirale’ und selbst ‘Logarithmische Spirale’ findet, eignen sich lediglich zur Ausschmückung, nicht aber zur wissenschaftlichen Herstellung von Implantaten und gekrümmten konischen Kupplungen. Ich möchte an dieser Stelle Herrn Dupin, meinen Professor für Spezielle Mathematik würdigen, der mir dieses Verständnis wie auch die Fähigkeit zur Generalisierung vermittelt hat.
3.5.5. Die dreidimensionale logarithmische Spirale
Ich erinnerte mich, dass die logarithmischen Spiralen die bemerkenswerte Eigenschaft der Winkelerhaltung besaßen. Da ich in den Büchern zur Erweiterung der logarithmischen Spirale durch die dritte Dimension jedoch nicht fündig wurde, musste ich zur strikten Anwendung der Eigenschaften der logarithmischen Spirale auf die gekrümmten Prothesenschäfte, ohne Rundungen und Glättungen, die Methoden, Formulierungen und schließlich die Übertragung in eine Programmiersprache entwickeln. “Gekrümmten Raum in Logarithmischer Spirale” nannte ich die globale Geometrie, in der alle Punkte des Implantats berechnet sind. Zur Übertragung dieser Punkte auf die Herstellung mit numerischen Maschinen komme ich auf die klassische Geometrie zurück, indem ich jeden dieser Punkte in den euklidischen Orthonormalraum projiziere.
Damals fiel mir auf, dass die meisten Weichtiere, Schnecken, Muscheln und andere, in einem spiralförmigen logarithmischen Raum beschrieben werden, ebenso wie Galaxien, trotz einiger Störungen.
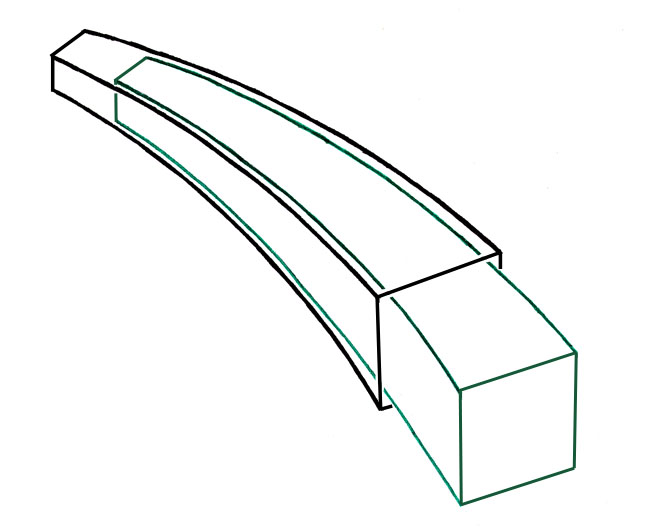
Nur ein in Gekrümmtem Raum in logarithmischer Spirale beschriebenes Implantat besitzt die Eigenschaft einer gekrümmten konischen Kupplung. Alle gekrümmten Implantate, die nicht mit dieser Geometrie berechnet werden, sind mit der Geometrischen Verankerung unvereinbar.
Ich entwickelte zwei Anwendungsgruppen der logarithmischen Spirale:
3.5.6. Die Gruppe der Schäfte
Die erste Gruppe, deren krummlinige Achse in einer Ebene liegt
Diese krummlinige Achse dient jeder Aufteilungsebene entlang der Achse als Bezugspunkt und besitzt einen lokalen Orthonormalraum, in dem alle zu dieser Ebene gehördenden Punkte definiert sind. Die Kanten der Schäfte, die mit den durch Raspelung oder Spiralräumen vorbereiteten Knochenwänden in Berührung kommen sollen, sind ebenfalls dreidimensionale logarithmische Spiralen, die sich regelmäßig von der krummlinigen Achse entfernen und konstante Winkel mit derselben bilden. Diese erste Gruppe liegt den unterschiedlichen Familien gekrümmter Schäfte zugrunde, die zu entwickeln ich Gelegenheit hatte.

Im Anhang 9.8.5. der ungekürzte Text meines Patents FR 96 01539 vom 08.02.1996
3.5.7. Die Gruppe der Räumer
Die zweite Gruppe besitzt eine krummlinige dreidimensionale Achse mit vielfachen Windungen beschrieben in einem Raum, in dem die Z-Koordinaten der aus der Aufteilung hervorgehenden Punkte selbst nach einer logarithmischen Funktion angeordnet sind. Diese Gruppe gekrümmter Räume ermöglichte mir die Entwicklung des Spiralräumers, der die Raspeln bei der Implantation der tiefen Modular-Plus-Reoperationsschäfte ersetzen sollte.
Im Anhang 9.8.7. der ungekürzte Text meines Patents EP 0 788 772 vom 08.02.1996
3.5.8. Diskretisierung der krummlinigen Achse
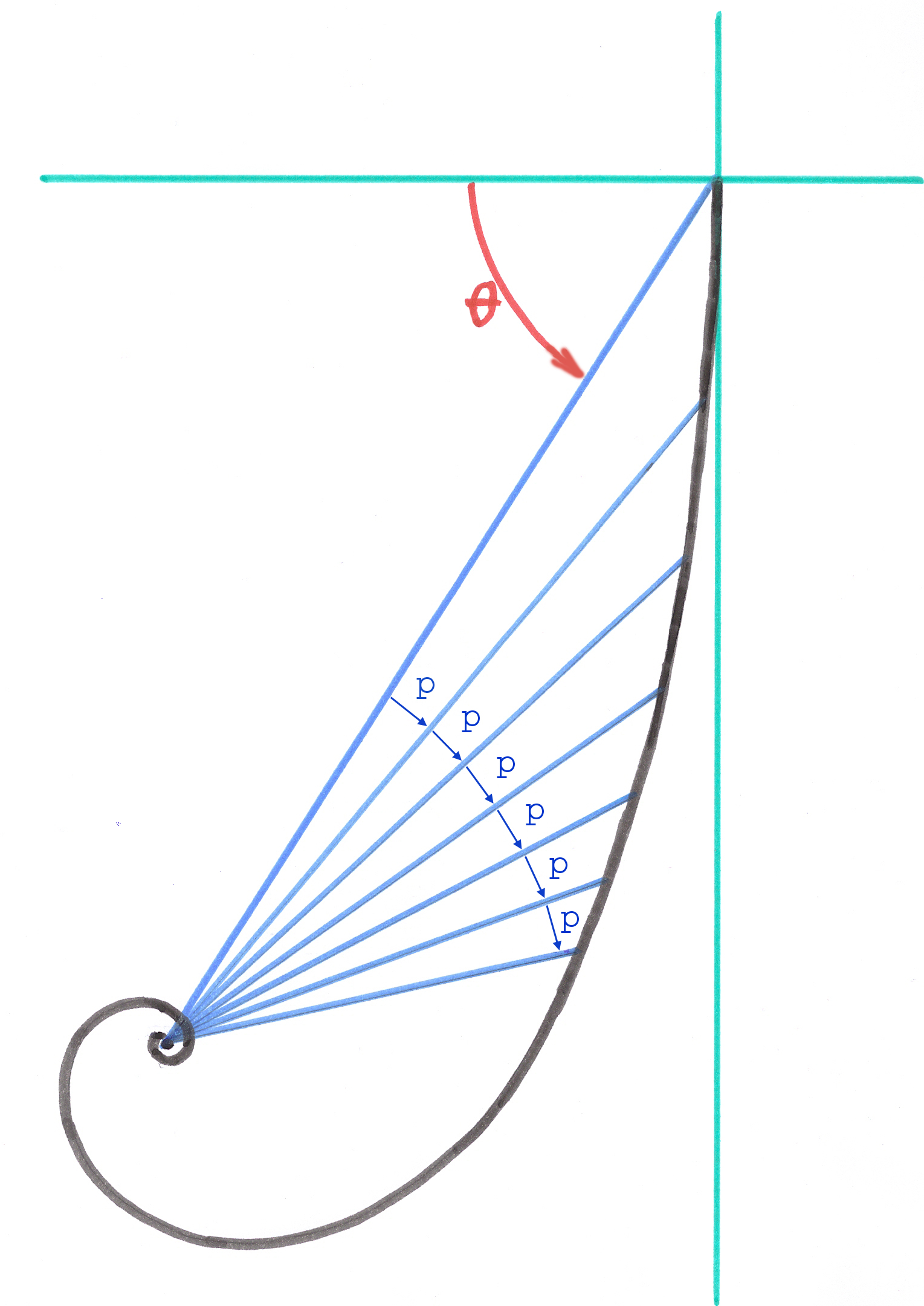
Die Verteilung dieser Kurven entlang der krummlinigen Achsen vollzieht sich nicht linear, sondern in konstanten Winkelschritten durch den Strahlenvektor, der dem Pol der Spirale entspringt und auf die krummlinige Achse trifft.
Die Gesamtkrümmung der mit dieser Methode berechneten gekrümmten Implantate muss sich auf ca. 0,2 Radiant beschränken.
3.5.9. Beschreibung eines Gegenstand in einem gekrümmten Raum in logarithmischer Spirale
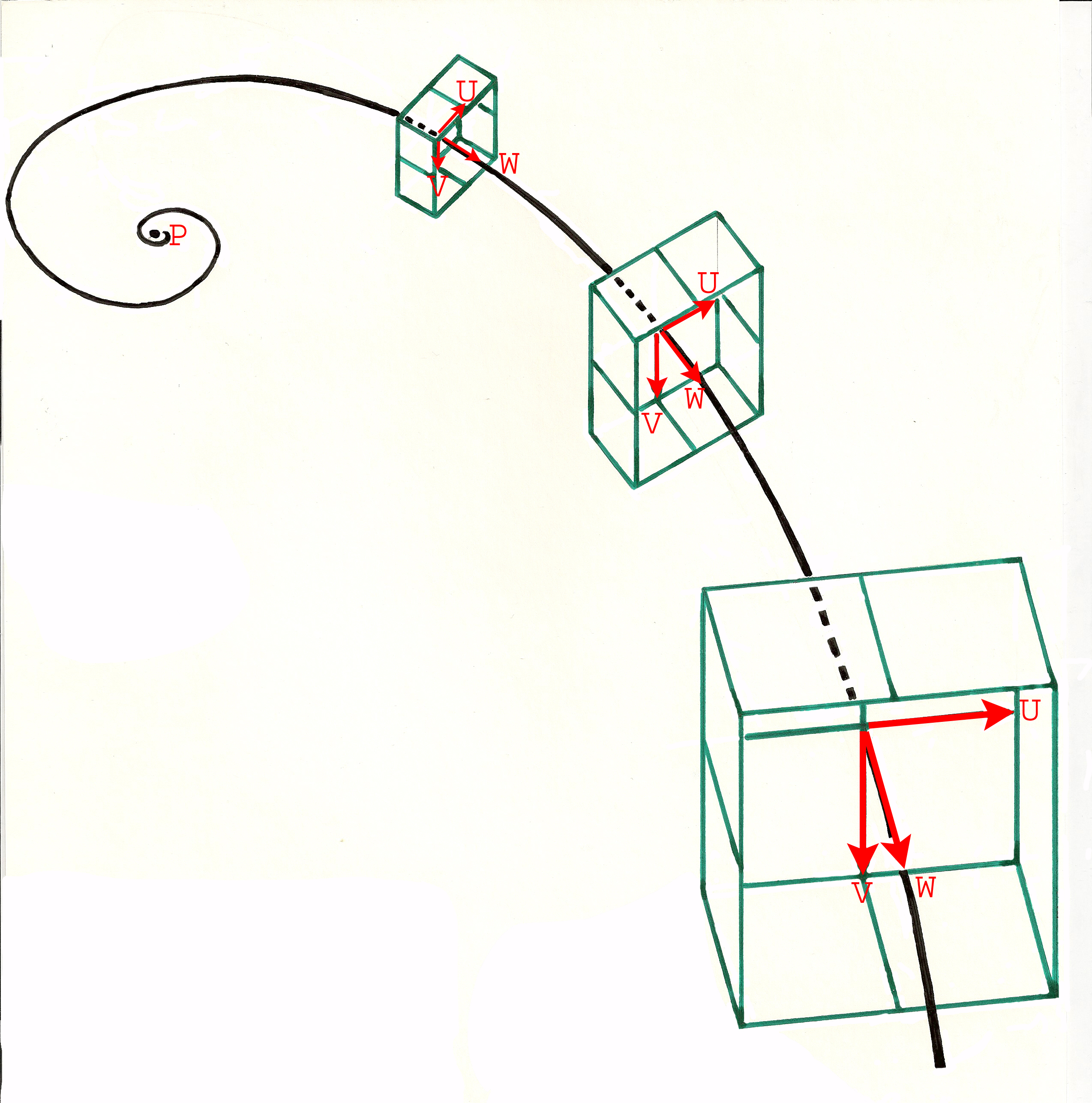
In jedem Punkt der nicht linearen Aufteilung der krummlinigen Achse ist ein lokaler, orthonormaler oder nicht orthonormaler, Vektorraum definiert, dessen zwei Vektoren U und V jedoch auf der Ebene senkrecht zur Achse liegen und dem durch zwei fortlaufende Punkte auf der krummlinign Achse definierten Vektor W untergeordnet sind. Dank der bemerkenswerten Eigenschaften der logarithmischen Spirale sind alle so definierten lokalen Vektorräume homothetisch.
Alle in diesen lokalen Räumen durch identische Koordinatensätze beschriebenen Gegenstandselemente sind gleichförmig, ihre Proportionen und vor allem ihre Winkel sind identisch. Im Fall der Modular-Plus-Schäfte sind die Querschnitte rechtwinkliger Form und die 4 Rillen in den lokalen Ebenen U und V definiert. Diese Vektoren U und V werden als senkrecht zum Lokalvektor W definiert, der durch zwei fortlaufende Punkte der Aufteilung auf der Spiralachse definiert ist, und ihre Normen sind identisch. Die Norm des Vektors W hängt dagegen von den Abständen der Aufteilung entlang der Achse ab, die nicht linear, sondern in logarithmischen Intervallen erfolgt.
Diese Intervalle entstehen durch die Schnittpunkte der Spiralachse mit Strahlenvektoren, die dem Pol entspringen und sich in konstanten Winkelschritten, definiert durch ein Parameter, fortbewegen.
3.5.10. In einem gekrümmten konischen Kanal implantierte Schäfte
Besitzt der lokale Schaftschnitt eine Rotationssymmetrie oder sind alle Querschnittspunkte, die sich auf den Knochen stützen, wie beim Modular-Schaft auf einem Kreis angeordnet, ist es äußerst wirksam, die Punkte der Schnittzeichnung als polare Lokalkoordinaten auf jeder Schnittebene zu definieren. Die Parameter, die diese Punkte in der Parameterbasis definieren, sind allen Schnitten der Aufteilung entlang des Schafts gemeinsam.
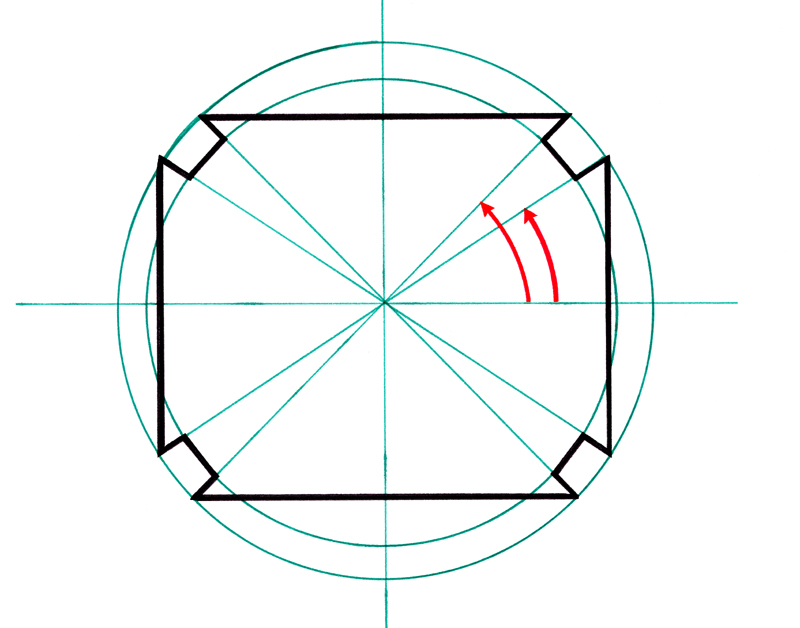
Wenn die laufenden Schnittpunkte in ihrem lokalen Raum berechnet werden, werden sie anschließend in den allgemeinen orthonormalen Millimeterraum projiziert, der zur Versorgung der Fräsprogramme der numerischen Herstellung bestimmt ist. Die für diese Projektion verwendeten Winkel erhält man aus der Orientierung des durch zwei fortlaufende Aufteilungspunkte der krummlinigen Achse begrenzten Lokalvektors W.
----
