3.6. Die Übergangs-Kurven
3.6.1. Zusammenfassung
Es handelt sich um eine Anzahl unterschiedlicher Modellierungsmethoden, die beispielsweise eine Verbesserung des Übergangs zwischen dem Proximalteil eines Oberschenkelknochenschafts und dem oberen Bereich des Oberschenkelhalses als Ersatz der traditionellen Kreisbögen ermöglichen.
Je nach ausgewähltem Implantatsbereich, der Suche nach dem besten mechanischen Widerstand unter Berücksichtigung des Metalls und seiner Bearbeitung, den mit der Begrenzung des in den Knochenbetten verfügbaren Raumes verbundenen Erfordernissen, den zur Vermeidung schädlicher Berührungen zwischen den beweglichen Bestandteilen zu treffenden Vorsichtsmaßnahmen, können die Übergangskurvenmodelle sehr unterschiedlich sein.
Schließlich kann die Übergangskurvenforschung in der Zukunft progressiv auf die Modellierung der immer komplexeren Bahnen der Knochenreihen ausgeweitet werden.
Ich habe mich mehrmals auf dieses Gebiet begeben und unebene Bahnen bei einigen Prothesenentwürfen eingeführt, die zur möglichst großen Annäherung an die Anatomie entwickelt wurden.
3.6.2. Die Suche nach besseren Modellen.
Bei meinen aufeinanderfolgenden Versuchen, die idealen Übergangskurven zwischen der Richtung der Achse eines Femurschafts und der Richtung des Halses zu finden, hatte ich die Gelegenheit, mehrere mathematische Modellierungen umzusetzen.
Bisher bewegte man sich im Maschinenbau fast ausnahmslos mit einem Kreisbogen von einer Richtung in die andere, um eine Schwächung eines Teils an der Stelle des Richtungswechsels zu vermeiden. Dies ist völlig in Ordnung, solange keine zusätzlichen Anforderungen an die Gestaltung des mechanischen Teils gestellt werden, wie z. B. Platz- oder Gewichtsbeschränkungen oder Konflikte mit einem anderen Teil. Selbst in der Luftkonstruktion gilt: Wenn ein Teil nicht stark genug ist, muss man es einfach größer und schwerer machen!
Andererseits ist es bei orthopädischen Implantaten aufgrund des begrenzten Platzes im Knochen des Patienten schwierig, eine Größe zu implantieren, die größer als die Markhöhle ist.
3.6.3. Übergangskurven und die Finite-Elemente-Methode
Die „Finite-Elemente“-Methode zur Analyse der Spannungen, denen mechanische Teile ausgesetzt sind, wird häufig zum Testen von Implantaten verwendet, die mit CAD-Software entworfen wurden. Ich habe diese Methode kennengelernt, indem ich die Kurse der Professoren Lavaste und Landjerit am Arts et Métiers in Paris besucht habe.
Mit dieser Methode ist es möglich, die Belastungen, denen ein mechanisches Teil ausgesetzt ist, zu simulieren und die Bereiche hervorzuheben, in denen das Teil überlastet ist und brechen kann. Anschließend wird das Teil ohne Berechnungen korrigiert oder neu konstruiert und die Methode erneut angewendet, um herauszufinden, ob die Korrekturen vorteilhaft waren. Beispielsweise vergrößern wir den Radius der Übergangsbögen leicht. Dies ist eine Methode zur nachträglichen Validierung einer bereits fertiggestellten Zeichnung.
Die Methode erfordert erhebliche Rechenressourcen und beinhaltet, obwohl sie computerisiert ist, zahlreiche vollkommen subjektive Parameter, die approximativ vom Bediener definiert werden.
Die Untersuchung eines dreidimensionalen Objekts mit der „Finite-Elemente“-Methode erfordert das Zerlegen dieses Objekts in kleine Elementarvolumina, beispielsweise Tetraeder, deren Seiten weder sehr klein noch unendlich klein sind, sondern „endliche“ Dimensionen haben. „bekannt, messbar und kalkulierbar.
Diese Aufteilung in kleine Elementarvolumina („Diskretisierung“) wird oft durch die Software automatisiert, und in diesem Fall ist das erhaltene Netz reichlich vorhanden, aber ungeordnet und unterliegt hauptsächlich der Auswahl von Dichte oder Abmessungen. Andererseits ist es auch möglich, die Mesh-Knoten manuell zu definieren, was besonders aufwändig ist. Es werden nur minimale Punkte eingegeben und die Genauigkeit der Ergebnisse ist geringer.
Oft verzichtet man auf das dreidimensionale Netz, um das Objekt nur im ebenen Schnitt zu untersuchen. Man extrapoliert die Ergebnisse durch logische Schlussfolgerungen auf die dritte Dimension, gehen dabei jedoch das Risiko grober wenn nicht riesigen Fehler ein.
Ein typisches Beispiel für diese Vereinfachung war die vergleichende Analyse von Zweymüller-Stäben durch HUISKES. Dieses Verfahren verschleierte die dritte Dimension, die dennoch der Ursprung der klinischen Überlegenheit der Zweymüller-Schäften ist.
Meine Philosophie besteht vielmehr darin, durch Reflexion und Theorie die Ergebnisse vorwegzunehmen, die man vorhersehbar mit der Finite-Elemente-Methode erzielen würde. Für die verschiedenen Bereiche der Implantate suchte ich nach günstigen und programmierbaren mathematischen Modellen.
Dadurch ist es möglich, die übermäßigen Approximationen der Finite-Elemente-Methode zu vermeiden. Eine Finite-Elemente-Prüfung ist danach immer interessant.
3.6.4. Die Kette
Bei einer Hüftprothese ist der intertrochantäre Bereich zwischen der proximalen Spitze des Schafts und dem Hals ein Bereich, in dem das Metall ständig einer Zugkraft durch die vom Kopf ausgehenden Belastungen ausgesetzt ist.
Es ist zu beachten, dass sich intramedulläre Schaftprothesen von der Realität der Architektur des natürlichen Femurs unterscheiden, da der Trochanter major, der ursprünglich mit dem natürlichen Hals verbunden war, nicht mehr mit dem Prothesenhals verbunden ist und eine kleine Grenze, die ich eher zuordne, nicht mehr mit dem Prothesenhals verbunden ist Auf die elastischen Bewegungen des Trochanter major als auf die Bewegungen des Stabes in der Diaphyse kann beobachtet werden.
Eine Ausnahme bildet das Beispiel der alten sogenannten „isoelastischen“ Schäfte von Robert Mathys, bei denen es notwendig war, den Trochanter durch eine Zugschraube mit dem Schaft zu verbinden, um zu versuchen, seine Hyperelastizität auszugleichen.
Eine Möglichkeit, diesen Bereich zu modellieren, besteht darin, sich in diesem Bereich eine „Diskretisierung“ durch Schichten vorzustellen (ohne es tatsächlich zu tun), das heißt durch die theoretische Aufteilung des Objekts zunächst in aufeinanderfolgende Schichten nach Art einer Zwiebel und dann durch Aufteilen jeder Schicht mit einem Netz.
Jede Schicht würde sich für sich betrachtet so verhalten, als ob sie einer Zugkraft wie eine gespannte Haut ausgesetzt wäre, während sie in Wirklichkeit an der darunter liegenden Metallmasse haften bleibt. Auf diese Weise würde jede Schicht idealerweise die Form einer „Kette“ annehmen.
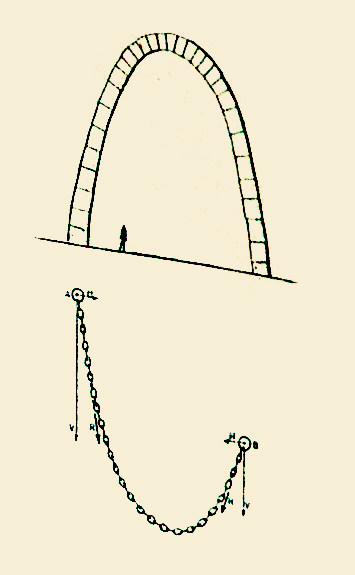
Die „Kette“ oder Katenoid ist die Kurve, die die Kette einer Halskette auf natürliche Weise annimmt, einerseits aufgrund der Schwerkraft an jedem der Glieder mit konstanter Masse und andererseits aufgrund der offensichtlichen Konstanz der Spannung an jedem Punkt entlang der Kette.

Aufgrund dieser Analogie wird die ebene Kurve mathematisch durch den hyperbolischen Kosinus der Form Y = CH X beschrieben mit: CH X = ( e^x + e^-x )/2 oder die Srienform, die ich verwendet habe: CH X = 1 + X^2/2! + X^4/4! + X^6/6! + X^8/8! + X^10/10! + usw...


3.6.5. Treffen mit Gaudi... ein Jahrhundert später
Kürzlich, im Jahr 1999, als die meisten meiner Prothesenprojekte abgeschlossen waren, wurde ich in Barcelona auf die erstaunlichen Werke von Antoni Gaudi (1852 – 1926) aufmerksam. Meine Zufriedenheit ergab sich aus der großen Analogie seines intellektuellen Ansatzes zur Behandlung von Übergangskurven mit dem, den ich 25 Jahre lang bei der Gestaltung von Übergangskurven und Oberflächen in Implantaten angewendet hatte. Ich war schon lange fasziniert von Kurvenfamilien, die allmählich von eckigen Formen zu abgerundeten Formen übergehen, die ich hier Übergangskurven nenne.
Der berühmte Architekt von Barcelona, Antoni Gaudi, hatte die unglaubliche Intuition, die Pläne der Kathedrale von Barcelona und der Gewölbe zahlreicher Gebäude zu zeichnen, indem er genau die umgekehrten Kettenformen übernahm, die seine Modelle aus feinen Schnüren, die aufgehängt an der Decke seiner Werkstatt waren.



3.6.6. Gaudi Forscher in Geometrie
In der Werkstatt neben seinem Büro entwickelte Gaudi ein echtes Forschungsprogramm zu Aspekten der Geometrie, die für seine Arbeit als Architekt wichtig sein könnten ... Er konzentrierte sich auf die experimentelle Suche nach optimalen geometrischen Lösungen, die er auf seine Projekte anwenden konnte. Krümmungen, Flächen und Transformationen interessierten ihn nur, wenn er sie in seinen Konstruktionen anwenden konnte. ...
Er schuf ein geometrisches Universum, um seiner eigenen Kreativität zu dienen. (Claudi Alsina i Català, Mark Burry, Gaudi Unseen, Jovis Berlin.)
Wenn die anderen Kathedralenbauer Gaudís Intuition gehabt hätten, wären Hunderte von Gebäuden heute keine Trümmerhaufen.
Für mehrere Implantatfamilien habe ich diese Kettenmodellierung der Zone gewählt, in der das Metall durch Zug beansprucht wird, indem ich die Koordinaten, die zuvor mit der hyperbolischen Kosinusfunktion berechnet wurden, in die Parameter einfügte, die die intertrochantäre Übergangskurve bis „an der Basis“ beschreiben die konische Verbindung mit dem Kopf.

3.6.7. La courbe de transition hyperbolique

Um den Übergang zwischen der Verankerungszone und dem zylindrischen Hals des AlloClassic-Stabs (1984) zu modellieren, suchte ich nach einer Kurve, die sehr allmählich aus der Verankerungszone austritt und deren Krümmung ist, da ich keine kreisbogenförmige Übergangskurve anwenden wollte, die mir zu umständlich erschien, variierte regelmäßig, um tangential die Basis des zylindrischen Halses zu erreichen.
Meine Anwendung des hyperbolischen Übergangs auf die AlloClassic-Schaftfamilie war Gegenstand meines Patents.. (6.2.6.).
Dank seiner hyperbelbogenförmigen Übergangskurve kam es beim AlloClassic-Schaft nur sehr selten zu Konflikten mit dem Kalkar im Bereich des Kragenschnitts. Diese Form wurde kritisiert, da die Füllung und der Kontakt zum Knochenbett in diesem Bereich in den Augen mancher zumindest auf frontalen Röntgenbildern nicht ausreichend erschien.
Dank der Geometrischen Verankerung ist der AlloClassic-Schaft durch seine Verankerungszone dennoch ausreichend stabilisiert, und ich glaube heute, dass es nicht unbedingt erforderlich war, dass die metaphysäre Füllung vollständiger war. Für die korrekte Ausnutzung der Impaktionsreserve war es statistisch sehr interessant, Konflikte selten zu machen, die 4 oder 5 Millimeter zusätzliche Impaktion verhindert hätten.
3.6.8. Exponentielle Übergangskurven
Da der AlloClassic-Schaft radiologisch manchmal keinen erkennbaren Kontakt zum Kalkar aufweist, wurde ich bei der Herstellung des SL Plus-Schafts gebeten, die Füllung des Kalkarbereichs zu erhöhen.
Für den SL Plus-Schaft habe ich eine mathematische Modellierung der Übergangskurve übernommen, bei der die Variation des Krümmungsradius entlang des Übergangsbogens einfacher parametrisiert werden konnte, während für das hyperbolische Modell des AlloClassic-Schaftes die maximale Krümmung immer bei die Basis des zylindrischen Halses lag.
Die Modellierung durch einen Teil einer Exponentialkurve, die in einem nicht orthonormalen lokalen Koordinatensystem definiert ist (siehe 4.3.2.), hat den Vorteil, dass sie an ihrem Startpunkt eine perfekte Tangente mit der Ankerzone aufweist, und ermöglicht es, mein Gesetz des Positiven Ableitungen zu erfüllen.
Diese Modellierung ermöglicht es auch, den Winkel der Tangente an die Kurve am Ankunftspunkt an der Basis des Verbindungskegels kontinuierlich zu parametrisieren. Diese Modellierung ersetzt den zylindrischen Teil des Halses vollständig. In der Praxis werden die Parameter dieser Kurve automatisch für jede Größe von einem Algorithmus in aufeinanderfolgenden Iterationen berechnet.
3.6.9. Die Methode des Raketenabschusses
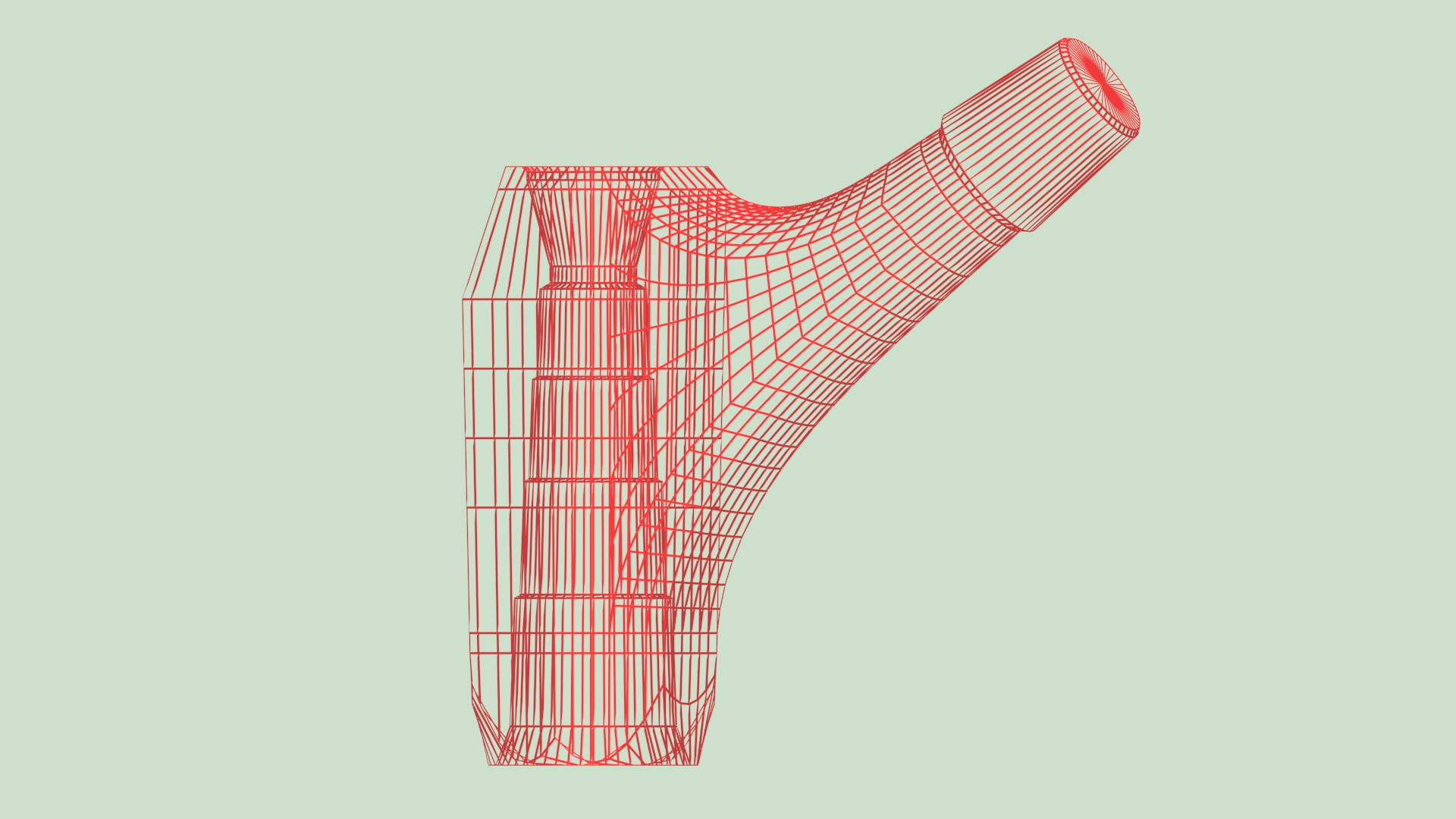
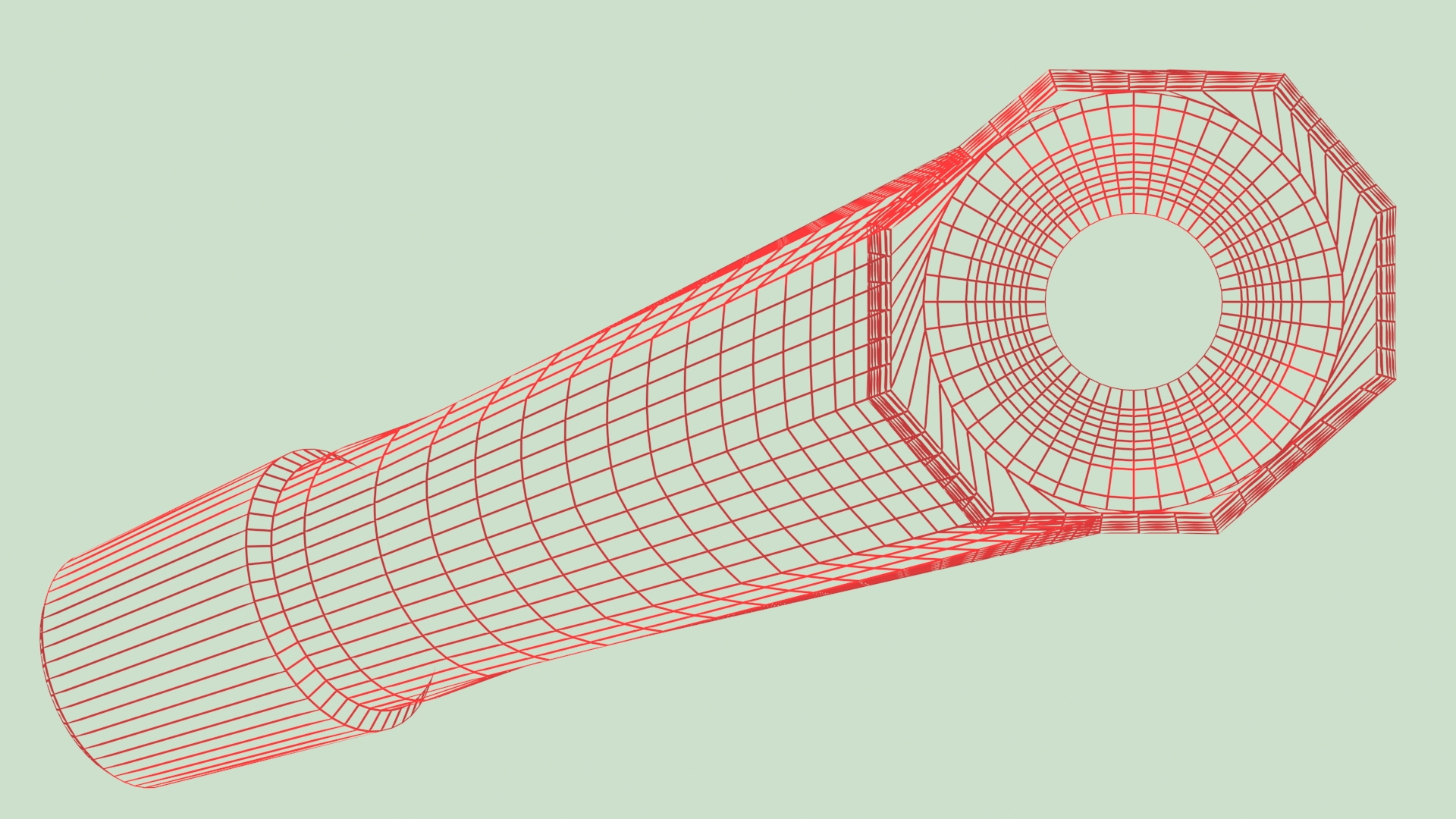
Zur Modellierung der proximalen Teile des Modular Plus-Systems habe ich eine automatische Berechnungsmethode angewendet. Die Links-Rechts-Symmetrie dieser Teile ermöglichte es, jede Kurve, die die Basis des proximalen Teils mit der Basis des Verbindungskegels verbindet, in einer vertikalen Ebene zu beschreiben. Die Fläche, die den medialen Teil der Basis des Teils mit der unteren Hälfte der Kegelbasis verbindet, besteht aus 24 nacheinander berechneten Kurven.
3.6.10. Die dreidimensionale Raketenschussmethode
Für die Modellierung der nicht symmetrischen links-rechts proximalen Teile des ANA.NOVA Projekts war es nicht mehr möglich, die ebenen Übergangskurven beizubehalten. Das neue Konzept der nach vorne versetzten Halsachse, das das Implantat noch näher an die reale Anatomie des proximalen Teils des Femurs bringt, erforderte die Verbindung von Schaft und Hals durch dreidimensionale Übergangskurven.
Diese Methode führt eine automatische Simulation der Orientierungslinien der kristallinen Komponenten des kortikalen Knochens und der Orientierung der Knochentrabekel der Spongiosa durch, die der Orientierung realer Beanspruchungen nahe kommt.
Die Erzeugung dieser Übergangskurven ist eine Modellierung analog zu den zielsuchender Raketen, die ein sich bewegendes Ziel verfolgen und nicht in der vertikalen Ebene des Schusses bleiben.
Um es etwas deutlicher auszudrücken: Der Weg vom Schaft zur Basis des Kegels ist in mehrere Segmente unterteilt. Durch eine automatische Iteration des Algorithmus werden die aufeinanderfolgenden Segmente schrittweise in 3D in Richtung des Ziels abgelenkt, um zum letzten Segment zu gelangen, das mit dem Zielsegment am Umfang des Kegels ausgerichtet wird, und dies auf 24 verschiedenen Trajektorien in 3D.

----
Nächste Kapitel : 4. Spezifische Methoden für Schäfte
