3.3. The Law of Positive Derivates
3.3.1. Summary
Through this language borrowed from mathematics, I express certain design rules for prosthetic stems. These rules make it possible to ensure good conditions for the progression of the dimensions and sections of the stems in the direction of the trajectory of its implantation.
Indeed, for the stems with Geometric Anchoring, the regular progression of the dimensions along the axis is essential to obtain the Conical Junction effect of the stem in the rectified medullary canal. For cemented stems, these rules make it possible to dominate the distribution and compression of the viscous cement during the driving. The Extractibility of all stems is facilitated by the application of these rules.
For the stems that I designed with numerical methods and whose coordinates of all the points are known, I established curves allowing to control graphically, throughout the development, the progression of the sections and the variations of this progress.
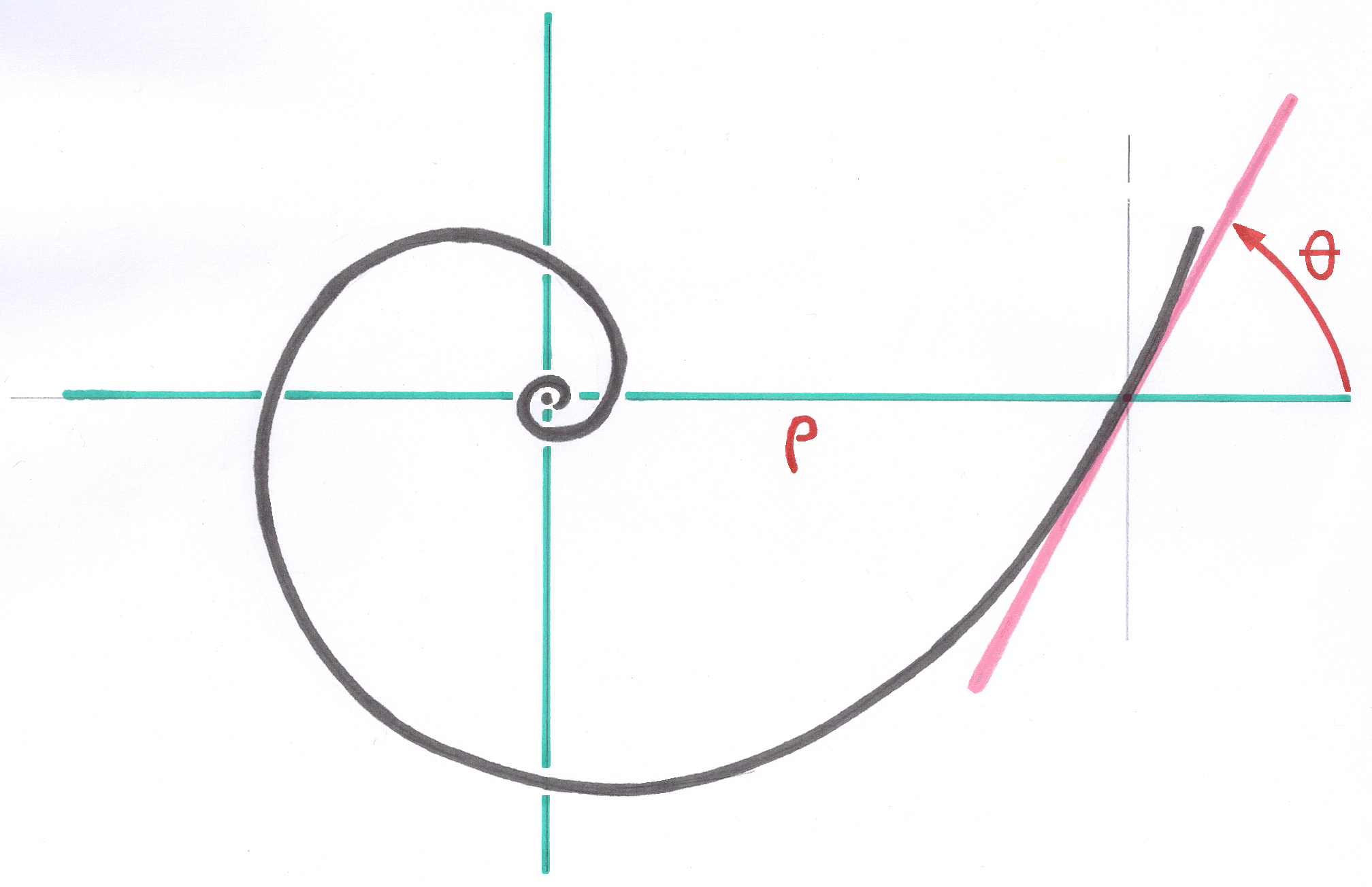
These notions apply to stems with a rectilinear axis and can be extended to stems with a curvilinear implantation axis ( In a Logarithmic Spiral Space).
In order not to weigh down this presentation, I have avoided any mathematical formalism.
3.3.2. This Law includes a set of rules of variations
This Law designates, in addition to the positive first derivatives themselves, a small set of conditions on the second derivatives, on each curve or additive function describing the stem, on the evolution of the surfaces of the cross sections all along the stem.
This Law expresses the need to have a continuous and positive variation all along the trajectory of implantation of a prosthesis satisfying the Geometric Anchorage.
I transposed several of these conditions also to the cemented stems to improve the distribution and compression of the cement during the implantation trajectory.
If we consider the axis of impaction of a cementless implant, rectilinear or curvilinear, along this axis, on the one hand the surface of the section must increase regularly from one end to the other of the zone of fixing, on the other hand the distance to the axis of all points of the sections must also increase regularly in all directions perpendicular to the axis.
The first derivative of the section must be positive and the second derivative continues in the anchor area. This notion must remain valid even if the axis of implantation or impaction is not a straight line in the strict sense but a regular curve such as, for example, a logarithmic spiral arc in the case of deep reoperation prostheses.
This leads to mathematical conditions on the nature of each additive curve which enters into the definition of the exact shape of the anchorage zone of the stem. Areas of the prosthesis that are not strictly part of the anchorage area must not be at least in contradiction with the Law of Positive Derivatives, such as typically the abruptly oblique trochanteric area of cemented Müller stems .
3.3.3. The AlloClassic stem simply satisfies this Law
A rectangular cross-section stem, like the AlloClassic stem, which consists only of the Pyramidal Base Shape, satisfies this Law in the simplest way.
The first derivatives of its medial, lateral, anterior and posterior contour are positive and their values correspond to the slopes of their angles with respect to the longitudinal axis. The edges being straight, these slopes do not vary and the second derivatives are therefore zero. If we consider the evolution of the cross section, its surface increases linearly, its first derivative is constant and its second derivative is zero. This is correct for the anchoring zone, the distal pyramid on the other hand presents a break in slope which was resolved a few years later by the Function of the Distal Ogive.
3.3.4. Curvilinear axis anchor stems satisfy this law
The anchor stems, such as the Modular Plus and the stems of the Ana Nova project, whose curvilinear axis is a logarithmic spiral arc and all the points of the anchoring zone are also calculated in a Logarithmic Spiral Curved Space, satisfy this Law without any compromise thanks to their great analogy with traditional conical surfaces and the conservation of all angles.
3.3.5. Extension of the Law of Positive Derivatives to cemented stems
I applied, nevertheless with asymmetrical parameters, to the tip of the cemented Holz-Zacher stems, a function of the same mathematical nature, which defines the Ski Distal contributing to the positioning of the tip in the direction of the medial cortex during insertion into the cement.
3.3.6. Influence of the Law of Positive Derivatives for the longitudinal grooves of Holz-Zacher stems
As in the cemented stems of Müller, the longitudinal grooves of the cemented prostheses of Holz-Zacher have a stabilizing role in the cement sleeve.
But in the Holz-Zacher prostheses, these grooves have a much more evolved role which allows the progressiveness of the increase in the surface of the cross sections. The grooves are deeper and wider distally and taper steadily proximally.
Thus, the grooves compensate for the increase in section brought by the Fixation Function whose amplitude is greater than that of cementless stems. Thanks to the grooves, the cross section varies more than the external shape of the stem to obtain a peripheral compression of the cement.
These grooves of variable depth make it possible to treat independently, on the one hand the adaptation of the cemented stem to the general shape of the medullary canal, and on the other hand the aptitude of the stem for the harmonious distribution of the cement, in particular of to avoid the rupture of continuity of the cement sheath by piston effect.
3.3.7. Graphical use of the Law when focusing stems
In my stem calculation program, a utility precisely calculates the section of the stem at each of the 100 levels of the longitudinal cutting.
I thus obtain the variation curve of the sections along the stem. From this curve, I calculate the first derivative curve of the variation of the section and the second derivative curve of the variation of this variation.
The graphic observation of these curves and their derivatives allowed me, by numerous cycles of recalculation of all the stems, to parameterize the depths of the grooves and the Fixation Function until complete satisfaction.
----