3.2. La Méthode des Tailles Optimisées
3.2.1. Résumé
Cette méthode permet de supprimer l'imperfection des séries de tiges dont les tailles sont échelonnées linéairement, où les écarts entre les petites tailles restent malgré tout grands, et les écarts entre les grandes tailles inutilement petits. Avec une série optimisée, un patient, quelque soit la taille de ses os, reçoit l'implant le plus proche de ses besoins.
3.2.2. Les Tailles Optimisées
Les Tailles Optimisées assurent, avec une série d’implants fabriqués en série, une adéquation optimale à chaque patient, avec un nombre restreint de tailles.
La variation entre les Tailles Optimisées par la méthode des Facteurs de Croissance, est progressive. Les petites tailles sont relativement rapprochées les unes des autres et les grandes tailles ont des écarts de plus en plus importants.
Cette méthode permet de supprimer l'imperfection des séries de tiges dont les tailles sont échelonnées linéairement, où les écarts entre les petites tailles restent malgré tout grands, et les écarts entre les grandes tailles inutilement petits.
Avec une série optimisée, un patient, quelque soit la taille de ses os, reçoit l'implant le plus proche de ses besoins. Il est évident que pour un patient de très petite taille, tant la préparation que le choix de l'implant doivent être plus précis que pour un patient de très grande taille.
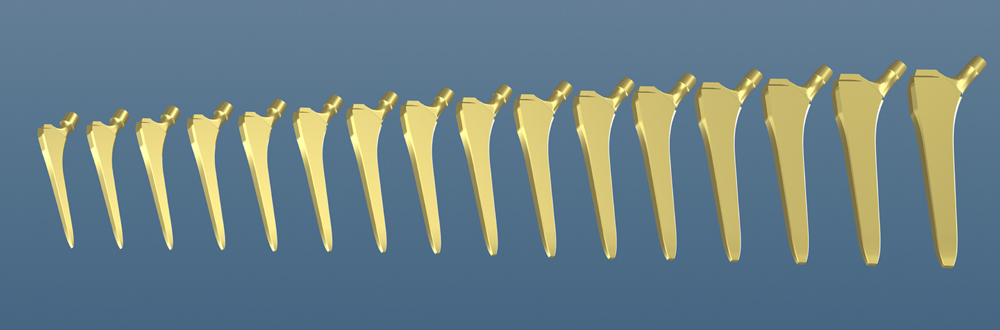
Pour garantir une cohérence entre la longueur et la largeur des tiges et satisfaire statistiquement la grande majorité des patients, j'ai mathématisé le problème par le procédé des Facteurs de Croissance, qui permet la création de séries de Tailles Optimisées.
Par cette méthode, les relations géométriques entre les diverses zones de l'implant restent conservées, et toutes les tailles de la série satisfont à toutes les lois de l'Ancrage Géométrique.
3.2.3. Critique des tailles non optimisées
Quand la conception des implants et des tailles est manuelle ou réalisée à l'aide des logiciels de dessin traditionnels, aucune relation n'est formulée entre les proportions de chaque implant. Aucune strategie de croissance n'est appliquée, sauf que chaque taille grandit en quelques zones, et diminue même parfois en d'autres zones.
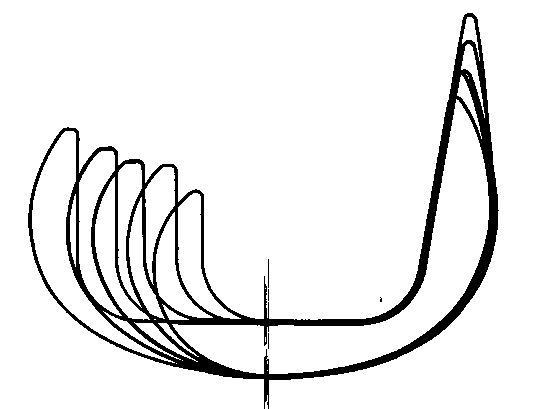
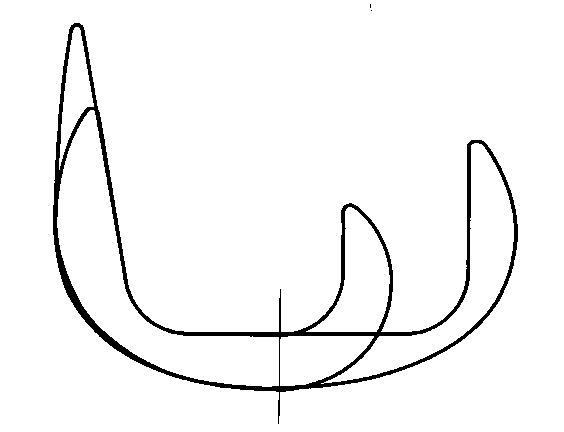
3.2.4. Echelonnement régulier des Tailles Optimisées

Mon paramétrage définissant la répartition des tailles tient surtout compte d'une longue expérience d'assistance opératoire et non de considérations abstraites :
1. Pour la plus petite et la plus grande taille, tous les critères importants, dont on désire tenir compte, doivent être définis en début de conception (longueur, largeur, épaisseur, longueur de col, etc...)
2. Ensuite le nombre de tailles de la série est défini par l'écart idéal admissible entre chaque taille afin que l'Opérateur ait la possibilité ( pour la hanche par exemple ) de positionner le haut de la prothèse, et donc le centre de la tête, à la hauteur idéale du point de vue orthopédique, et ainsi pouvoir reconstituer toutes les longueurs osseuses totales souhaitables avec une quasi continuité.
3. En exploitant la propriété d'Emboîtement Ascendant des implants et en ayant la possibilité d'ajuster la profondeur de râpage, l'Opérateur peut atteindre toute position intermédiaire.
Depuis la création de ma prothèse SL AlloClassic en 1984, à ma connaissance, aucune critique sur l'écart entre les tailles, ou sur l'absence d'une taille intermédiaire manquante, n'a été exprimée. Je peux donc considérer, à presque de 40 ans de recul, que la méthode des Tailles Optimisées a définitivement résolu ce problème.

3.2.5. Tailles Optimisées et distribution de Gauss
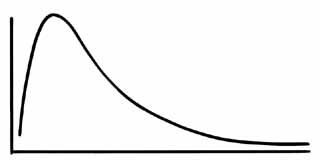
Lorsqu'on établit l'histogramme de la fréquence d'implantation des tailles d'une série d'implants optimisés, on obtient une distribution en courbe en cloche de Gauss.
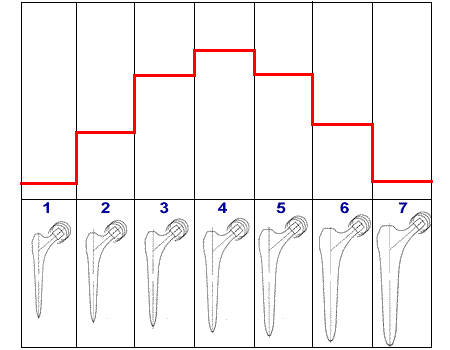
Cette distribution selon un histogramme en forme de courbe en cloche de Gauss peut servir à orienter les mises en stock des tailles au bloc opératoire, la gestion des stocks et les mises en fabrication chez les producteurs.
3.2.6. Les Tailles Optimisées rencontrent de rares exceptions
Comme pour toutes les prothèses fabriquées en série, les prothèses dont les tailles sont optimisées, tout en étant statistiquement bien adaptées à tous les patients, présentent quelques limites dans 1 à 2 % des cas.
L'exemple typique (que j'ai effectivement observé) est le cas d'un patient jeune, 40 ans environ, très actif et plutôt grand. Sa corticale est très épaisse et le diamètre du canal médullaire petit. Par conséquent, ce patient ne peut recevoir qu'une tige de petite taille parmi la série optimisée. Comme les longueurs de cols sont également variables et statistiquement adaptées aux tailles des patients, la longueur de col que ce patient recevra sera insuffisante
Néanmoins, ces cas sont prévisibles et planifiables et plusieurs options restent à la disposition de l'opérateur :
a) implanter une taille au-dessus car la série d'implants possède la propriété de l'Emboîtement Ascendant, et décider de râper plus longuement pour implanter la taille supérieure. La conception des râpes permet toujours de poursuivre la préparation du canal médullaire (10 cycles de râpage). C'est l'attitude que je conseille.
b) utiliser, à titre exceptionnel, une tête à col extra long
c) implanter le cotyle moins profondément ou utiliser un insert latéralisé
Pour ces cas particuliers, si ces options ne conviennent pas, la série des Tailles Optimisées ne concurrence pas les implants fabriqués sur mesure.
3.2.7. Application de la Méthode des Tailles Optimisées aux cotyles
Le concept des Tailles Optimisées a également une grande importance dans la conception des cotyles. En effet, les cotyles vissés sans ciment de Zweymüller de 1986 présentaient une distribution de dimensions très irrégulière.
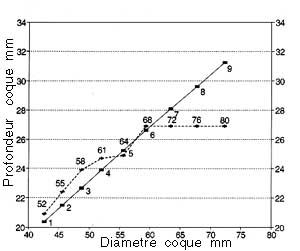
J'ai résolu ce problème avec le cotyle Bicon Plus de 1992 dont les 9 tailles de coques sont calculées en appliquant le principe des Tailles Optimisées grâce au procédé mathématique des Facteurs de Croissance.
D’une taille la suivante, les diamètres principaux et la profondeur totale de la coque varient avec un accroissement indépendant l’un de l’autre.
Les coques de très petite taille sont de conformation plus profonde et plus " sphériques ", et les coques de grande taille apparaissent plus aplaties, soit plus " elliptiques ". Il ne s’agit en aucun cas d’une croissance homothétique où toutes les dimensions varieraient avec le même facteur.
3.2.8. Historique du procédé des Tailles Optimisées
A l'occasion de ma participation en 1965 chez Carl Zeiss à un travail de recherche sur la vitesse de combustion des fusées à poudre, j'ai pu me rendre compte de l'importance du mode de classification des grains, particules ou objets quand on doit étudier leur répartition statistique.
Avec un histogramme subdivisé en classes linéaires, aucune conclusion ne pouvait être obtenue.
Avec un histogramme subdivisé en classes logarithmiques par contre, les grains de poudre ( ressemblant à des petits macaroni creux ) pouvaient être classés par leur taille ainsi que par leur surface de combustion, et des conclusions positives ont pu être tirées.
Dix ans plus tard, en 1974, également chez Carl Zeiss, j'ai eu à nouveau l'opportunité de constater les avantages de l'histogramme logarithmique par rapport à l'histogramme linéaire. A l'Institut de Recherche sur les Maladies Osseuses, Institut Calot à Berck-Plage, j'ai participé à une étude sur l'ostéoporose et l'efficacité de ses traitements, comme la calcitonine par exemple.
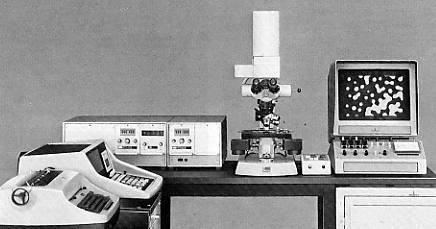
Pour cette étude, j'ai installé un grand microscope de recherche relié à l'analyseur d'images " Microvidéomat " de Carl Zeiss et un ordinateur pour lequel j'ai réalisé la partie théorique et toute la programmation, encore en " langage machine " à l'époque.
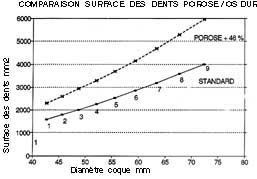
L'étude comportait la mesure de la surface des cellules osseuses sur des coupes minces polies de biopsies. J'avais programmé la présentation des résultats des mesures sous forme d'histogrammes sur mille cellules par patient, avec des classes non linéaires mais logarithmiques.
Comme les écarts-types des populations de cellules étaient du même ordre de grandeur que les différences à observer sur les histogrammes, avant ou après traitement, seule la classification logarithmique a permis d'observer concrètement les résultats.
La transposition de ces réflexions mathématiques aux séries de prothèses n'a pas été évidente. Paradoxalement, ce sont ici les tailles de prothèses qui constituent les classes dans lesquelles les patients sont distribués. Ce sont les patients, et dans l'exemple de la hanche, les formes et dimensions de la cavité médullaire de la partie proximale de leur fémur qui constituent la population à classer en histogramme.
----
